Capítulo 5: Visualización de Datos en Python
La Importancia de la Visualización
La visualización de datos es una herramienta fundamental en el proceso de análisis de datos. Una buena visualización puede revelar patrones, tendencias y anomalías que podrían pasar desapercibidos en tablas de datos crudos. Como dijo Edward Tufte, uno de los pioneros en visualización de información:
"La excelencia gráfica es la que da al espectador la mayor cantidad de ideas en el menor tiempo con la menor cantidad de tinta en el menor espacio."
En la ciencia de datos, la visualización cumple varias funciones críticas:
- Exploración de datos: Permite identificar rápidamente patrones, tendencias y valores atípicos durante el análisis exploratorio.
- Comunicación de resultados: Facilita la transmisión eficaz de hallazgos a diferentes audiencias, desde técnicas hasta no técnicas.
- Toma de decisiones: Proporciona información visual que ayuda a los stakeholders a tomar decisiones informadas.
- Validación de modelos: Permite evaluar visualmente el rendimiento y las predicciones de los modelos de machine learning.
Bibliotecas de Visualización en Python
Python ofrece un ecosistema rico de bibliotecas de visualización, cada una con sus propias fortalezas y características. En este capítulo, exploraremos las tres más importantes:
Matplotlib: La Biblioteca Fundamental
Matplotlib es una biblioteca de visualización completa para Python, inspirada en los gráficos de MATLAB. Fue creada por John D. Hunter en 2003 y se ha convertido en la base sobre la cual se construyen muchas otras bibliotecas de visualización en Python como Seaborn, pandas plotting y plotly.
Matplotlib ofrece un control detallado sobre cada aspecto de un gráfico, desde los elementos más básicos hasta personalizaciones avanzadas, lo que la hace extremadamente flexible pero a veces verbosa para tareas complejas.
Instalación de Matplotlib
Antes de comenzar a crear visualizaciones, necesitamos instalar Matplotlib. Lo podemos hacer fácilmente con pip:
# Instalar Matplotlib con pip
pip install matplotlibSi estás utilizando Anaconda, Matplotlib ya viene incluido en la distribución. Para verificar la versión instalada, puedes ejecutar:
# Verificar la versión de Matplotlib
import matplotlib
print(matplotlib.__version__)Importar la Biblioteca
Existen diferentes formas de importar Matplotlib. La más común es importar el submódulo pyplot, que proporciona una interfaz similar a MATLAB:
# Forma estándar de importar Matplotlib
import matplotlib.pyplot as plt
# Para mostrar gráficos en notebooks de Jupyter
%matplotlib inline
# Para gráficos interactivos en notebooks
%matplotlib widget # Requiere ipymplplt es una convención ampliamente utilizada al importar matplotlib.pyplot. Facilita la escritura de código y lo hace más consistente con las prácticas de la comunidad.
Comandos Básicos de Matplotlib
Veamos cómo crear un gráfico simple con Matplotlib:
# Importar las bibliotecas necesarias
import matplotlib.pyplot as plt
import numpy as np
# Crear datos de ejemplo
x = np.linspace(0, 10, 100) # 100 puntos entre 0 y 10
y = np.sin(x) # Función seno
# Crear un gráfico simple
plt.figure(figsize=(8, 4)) # Tamaño de la figura en pulgadas
plt.plot(x, y) # Crear la línea
plt.title('Función Seno') # Añadir título
plt.xlabel('x') # Etiqueta del eje x
plt.ylabel('sen(x)') # Etiqueta del eje y
plt.grid(True) # Mostrar cuadrícula
plt.show() # Mostrar el gráfico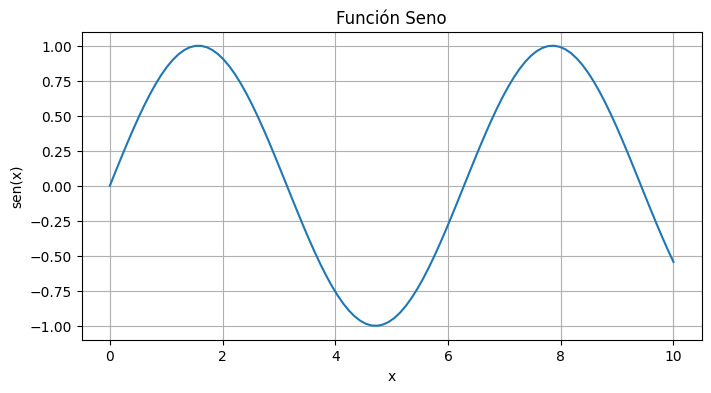
Matplotlib tiene dos interfaces principales:
- Interfaz pyplot (procedural): Similar a MATLAB, donde las funciones como
plt.plot()actúan sobre la figura "actual". - Interfaz orientada a objetos: Más flexible y explícita, donde se trabaja directamente con objetos como Figure y Axes.
El ejemplo anterior utiliza la interfaz pyplot. Veamos el mismo gráfico usando la interfaz orientada a objetos:
# Usando la interfaz orientada a objetos
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(x, y)
ax.set_title('Función Seno')
ax.set_xlabel('x')
ax.set_ylabel('sen(x)')
ax.grid(True)
plt.show()Personalización de Gráficos
Matplotlib ofrece un control detallado sobre prácticamente todos los elementos de un gráfico. Veamos cómo personalizar diferentes aspectos:
Título
El título es uno de los elementos más importantes de un gráfico. Puedes personalizarlo con diferentes opciones:
# Personalización del título
plt.figure(figsize=(8, 4))
plt.plot(x, y)
# Título básico
plt.title('Función Seno')
# Título con más opciones
plt.title('Función Seno: f(x) = sen(x)',
fontsize=16, # Tamaño de fuente
fontweight='bold', # Peso de la fuente: 'normal', 'bold', etc.
color='navy', # Color del texto
loc='center', # Posición: 'center', 'left', 'right'
pad=20) # Espacio en puntos entre el título y el gráfico
plt.plot(x, y)
plt.grid(True)
plt.show()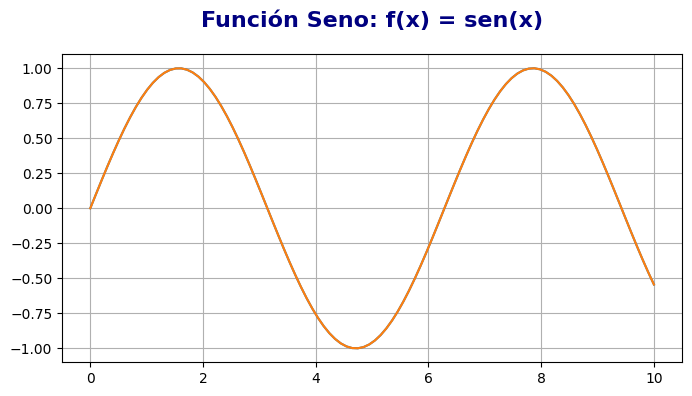
Nombres de los Ejes
Etiquetar correctamente los ejes es fundamental para que un gráfico sea comprensible:
# Personalización de etiquetas de ejes
plt.figure(figsize=(8, 4))
plt.plot(x, y)
# Etiquetas básicas
plt.xlabel('Tiempo (s)')
plt.ylabel('Amplitud')
# Etiquetas con más opciones
plt.xlabel('Tiempo (s)',
fontsize=12,
color='darkred',
labelpad=10) # Espacio entre la etiqueta y el eje
plt.ylabel('Amplitud',
fontsize=12,
color='darkred',
labelpad=10)
plt.title('Función Seno')
plt.grid(True)
plt.show()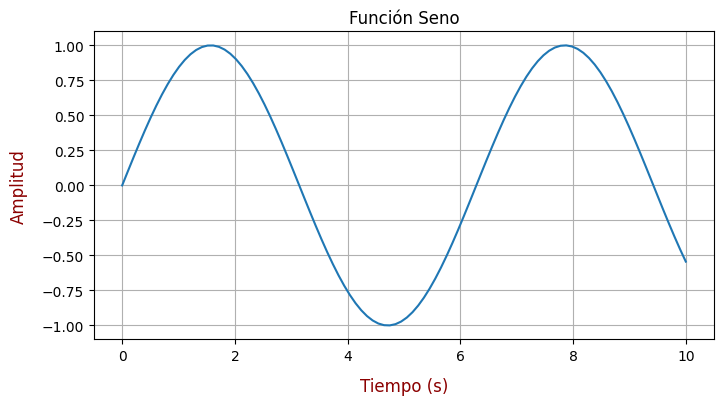
Para añadir fórmulas matemáticas en las etiquetas, puedes usar la sintaxis de LaTeX:
# Etiquetas con fórmulas matemáticas (LaTeX)
plt.figure(figsize=(8, 4))
plt.plot(x, y)
plt.xlabel('Ángulo ($\\theta$)')
plt.ylabel('$\\sin(\\theta)$') # Notación matemática
plt.title('$f(\\theta) = \\sin(\\theta)$')
plt.grid(True)
plt.show()$. En cadenas de Python, necesitas escapar el backslash, por lo que \alpha se escribe como \\alpha.
Legend (Leyenda)
Las leyendas son esenciales cuando tienes múltiples series de datos en un gráfico:
# Añadir leyendas a gráficos
plt.figure(figsize=(8, 4))
# Graficar múltiples líneas con etiquetas
plt.plot(x, np.sin(x), label='sen(x)')
plt.plot(x, np.cos(x), label='cos(x)')
plt.plot(x, np.exp(-x/3), label='$e^{-x/3}$')
# Añadir leyenda básica
plt.legend()
# O leyenda con más opciones
plt.legend(
loc='upper right', # Ubicación: 'best', 'upper right', 'center left', etc.
frameon=True, # Mostrar borde
fancybox=True, # Esquinas redondeadas
shadow=True, # Sombra
fontsize=10, # Tamaño de fuente
ncol=1 # Número de columnas
)
plt.title('Múltiples Funciones')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.show()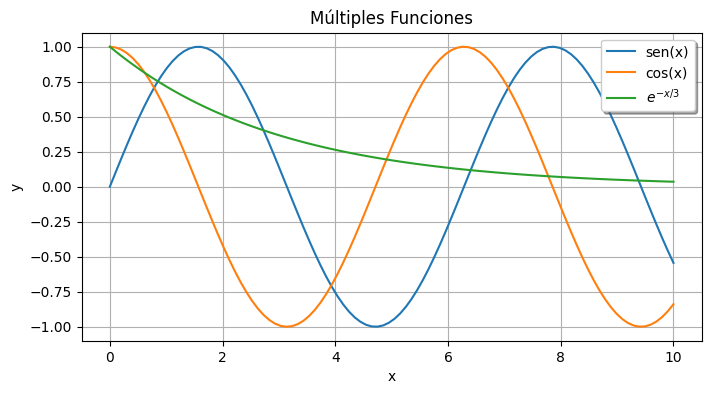
label cuando creas un elemento en el gráfico, ese elemento no aparecerá en la leyenda aunque llames a plt.legend().
Cuadrícula (Grid)
La cuadrícula puede ayudar a leer valores con mayor precisión y mejorar la legibilidad del gráfico:
# Personalización de la cuadrícula
plt.figure(figsize=(8, 4))
plt.plot(x, np.sin(x))
# Cuadrícula con más opciones
plt.grid(
visible=True, # Mostrar cuadrícula
which='both', # 'major', 'minor', 'both'
axis='y', # 'x', 'y', 'both'
linestyle='--', # Estilo de línea: '-', '--', '-.', ':'
linewidth=0.5, # Ancho de línea
alpha=0.7, # Transparencia
color='red' # Color
)
plt.title('Función Seno con Cuadrícula Personalizada')
plt.xlabel('x')
plt.ylabel('sen(x)')
plt.show()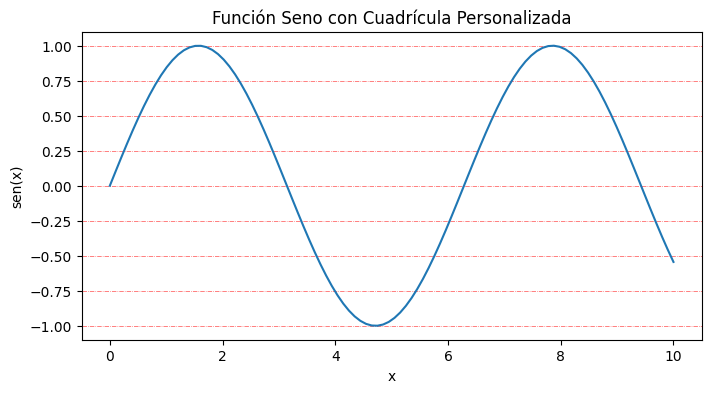
Más Opciones de Personalización
Tamaño de la Figura y DPI
El tamaño y la resolución de la figura son aspectos importantes, especialmente cuando necesitas gráficos para publicaciones o presentaciones:
# Configuración del tamaño y resolución
# figsize: (ancho, alto) en pulgadas
# dpi: puntos por pulgada (resolución)
plt.figure(figsize=(8, 4), dpi=100) # Figura de 8x4 pulgadas a 100 dpi
plt.plot(x, np.sin(x))
plt.title('Figura de 8x4 pulgadas a 100 dpi')
plt.show()
plt.figure(figsize=(4, 3), dpi=150) # Figura más pequeña con mayor resolución
plt.plot(x, np.sin(x))
plt.title('Figura de 4x3 pulgadas a 150 dpi')
plt.show()figsize) afecta las proporciones y el espacio disponible para el gráfico, mientras que el DPI (dpi) controla la resolución del gráfico exportado. Para proyectos web, 100 dpi suele ser suficiente, mientras que para publicaciones académicas se recomienda 300 dpi o más.
Parámetros de las Líneas: Colores, Ancho y Tipos
Matplotlib ofrece muchas opciones para personalizar el aspecto de las líneas en tus gráficos:
# Personalización de líneas
plt.figure(figsize=(10, 6))
# Diferentes estilos de línea
plt.plot(x, np.sin(x),
color='blue', # Color por nombre
linestyle='-', # Estilo de línea: sólida
linewidth=2, # Ancho de línea
marker='o', # Marcador: círculo
markersize=6, # Tamaño del marcador
markerfacecolor='white', # Color interior del marcador
markeredgecolor='blue', # Color del borde del marcador
markeredgewidth=1.5, # Ancho del borde del marcador
alpha=0.7, # Transparencia
label='sin(x) - detallado')
# Forma simplificada usando la sintaxis abreviada
plt.plot(x, np.cos(x), 'r--', linewidth=2, label='cos(x) - simplificado')
# Tercera línea con otro estilo
plt.plot(x, np.sin(x) * np.cos(x), 'g-.', linewidth=1.5, label='sin(x)cos(x)')
plt.title('Diferentes Estilos de Línea')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()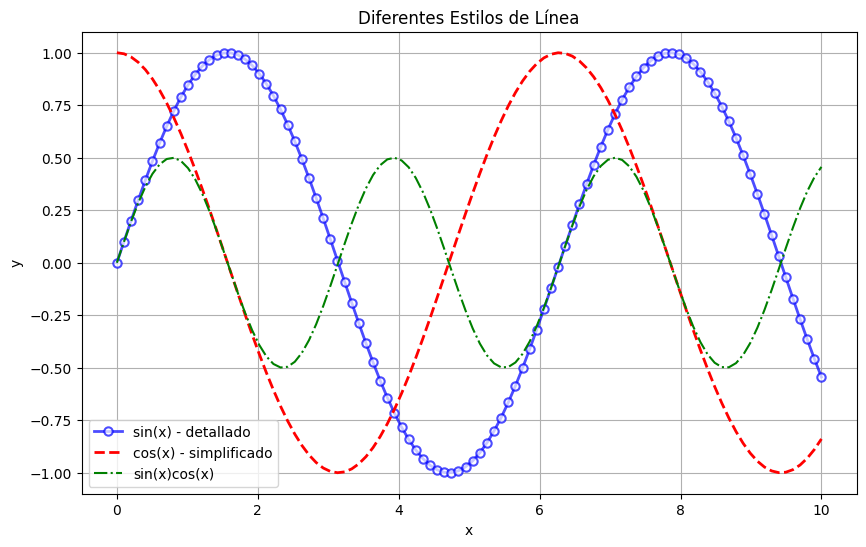
La sintaxis abreviada para definir líneas combina color, marcador y estilo en un solo string:
# Demostración de la sintaxis abreviada
plt.figure(figsize=(12, 8))
# Diferentes combinaciones de color, marcador y estilo
estilos = [
'b-', 'r--', 'g-.', 'c:', 'm-o', 'y-^', 'k-s',
'b--o', 'r-+', 'g:*', 'c-d', 'm--p', 'y-.h'
]
# Crear múltiples líneas con diferentes estilos
for i, estilo in enumerate(estilos):
plt.plot(x, np.sin(x + i*0.5), estilo, label=f'Estilo: {estilo}')
plt.title('Demostración de Estilos de Línea')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(ncol=2) # Leyenda con 2 columnas
plt.grid(True)
plt.show()Opciones comunes para la sintaxis abreviada
| Colores | 'b' (blue), 'g' (green), 'r' (red), 'c' (cyan), 'm' (magenta), 'y' (yellow), 'k' (black), 'w' (white) |
| Marcadores | '.' (punto), 'o' (círculo), 'v' (triángulo abajo), '^' (triángulo arriba), 's' (cuadrado), '+' (más), 'x' (equis), '*' (estrella) |
| Líneas | '-' (sólida), '--' (discontinua), '-.' (punto y raya), ':' (punteada) |
Subplots: Múltiples Gráficos
Los subplots permiten crear múltiples gráficos en una sola figura, lo que es útil para comparar diferentes conjuntos de datos o visualizar diferentes aspectos de los mismos datos.
Creación Básica de Subplots
# Crear una cuadrícula simple de subplots (2 filas, 2 columnas)
fig, axs = plt.subplots(2, 2, figsize=(10, 8))
# Graficar en cada subplot
axs[0, 0].plot(x, np.sin(x))
axs[0, 0].set_title('Seno')
axs[0, 0].grid(True)
axs[0, 1].plot(x, np.cos(x), 'g-')
axs[0, 1].set_title('Coseno')
axs[0, 1].grid(True)
axs[1, 0].plot(x, np.tan(x), 'r-')
axs[1, 0].set_title('Tangente')
axs[1, 0].set_ylim(-5, 5) # Limitar el rango del eje y
axs[1, 0].grid(True)
axs[1, 1].plot(x, np.exp(x), 'm-')
axs[1, 1].set_title('Exponencial')
axs[1, 1].grid(True)
# Ajustar el espaciado entre subplots
plt.tight_layout()
# Añadir un título para toda la figura
fig.suptitle('Funciones Matemáticas Básicas', fontsize=16, y=1.02)
plt.show()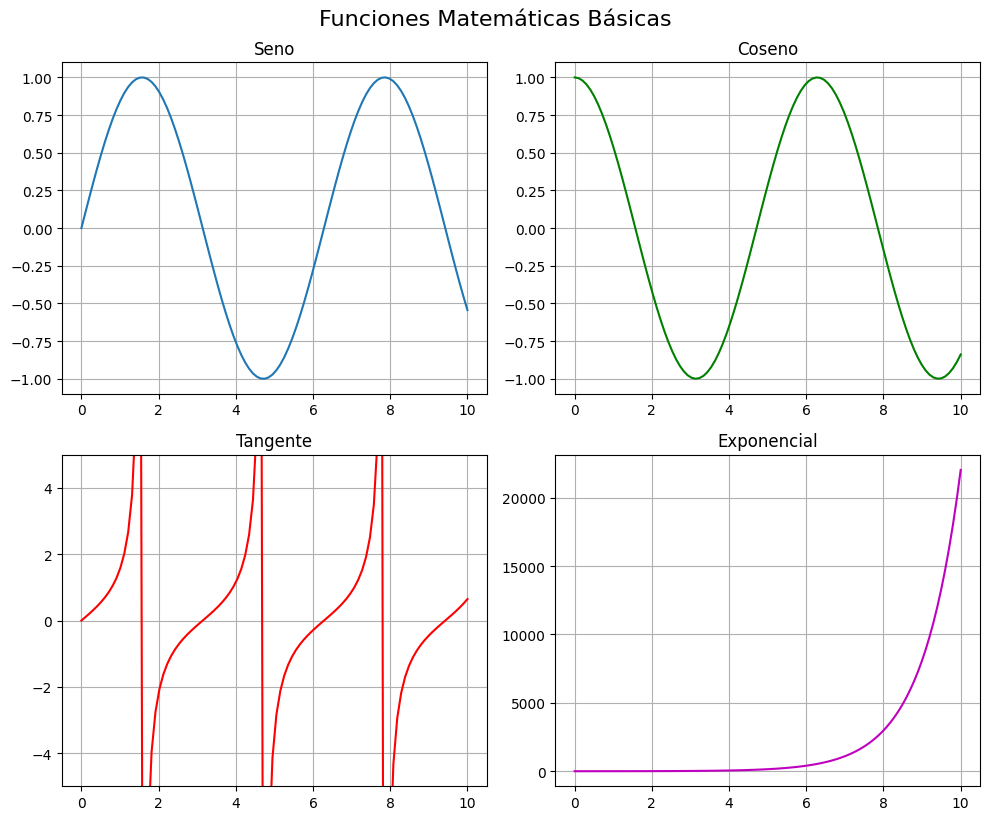
Rango del Plot
Controlar el rango de los ejes es fundamental para resaltar características específicas de tus datos:
# Controlar el rango de los ejes
plt.figure(figsize=(10, 6))
# Crear datos para graficar
x = np.linspace(-2*np.pi, 2*np.pi, 1000)
y = np.sin(x)
plt.plot(x, y)
plt.title('Función Seno con Rango Personalizado')
plt.xlabel('x')
plt.ylabel('sen(x)')
# Establecer límites personalizados para los ejes
plt.xlim(-np.pi, np.pi) # Limitar el eje x de -π a π
plt.ylim(-1.2, 1.2) # Dar un poco de espacio en el eje y
# Añadir líneas en x=0 y y=0
plt.axhline(y=0, color='k', linestyle='--', alpha=0.7) # Línea horizontal en y=0
plt.axvline(x=0, color='k', linestyle='--', alpha=0.7) # Línea vertical en x=0
plt.grid(True)
plt.show()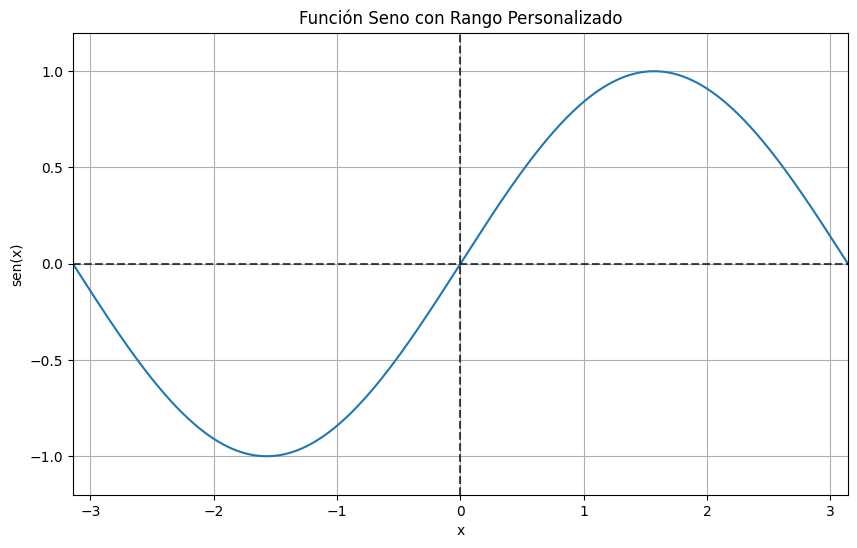
Anotaciones de Texto
Las anotaciones de texto permiten destacar puntos específicos o características importantes en un gráfico:
# Añadir anotaciones de texto a un gráfico
plt.figure(figsize=(10, 6))
x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x)
plt.plot(x, y, 'b-')
plt.title('Función Seno con Anotaciones')
plt.xlabel('x')
plt.ylabel('sen(x)')
plt.grid(True)
# Marcar puntos específicos
puntos_x = [0, np.pi/2, np.pi, 3*np.pi/2, 2*np.pi]
puntos_y = [np.sin(x_val) for x_val in puntos_x]
plt.plot(puntos_x, puntos_y, 'ro', markersize=8)
# Añadir texto simple
plt.text(0.1, 0.8, 'Función Seno', fontsize=12)
# Añadir anotaciones con flechas
plt.annotate('Máximo',
xy=(np.pi/2, 1), # Punto a señalar
xytext=(np.pi/2, 1.3), # Posición del texto
arrowprops=dict(facecolor='black', shrink=0.05, width=1.5))
plt.annotate('Mínimo',
xy=(3*np.pi/2, -1),
xytext=(3*np.pi/2, -1.3),
arrowprops=dict(facecolor='black', shrink=0.05, width=1.5))
plt.annotate('Punto de inflexión',
xy=(np.pi, 0),
xytext=(np.pi + 0.5, 0.3),
arrowprops=dict(facecolor='red', linewidth=1.5, arrowstyle='->'))
# Añadir una formula matemática
plt.text(np.pi/4, -0.5, r'$\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}$',
fontsize=14, bbox=dict(facecolor='white', alpha=0.7))
plt.ylim(-1.5, 1.5)
plt.show()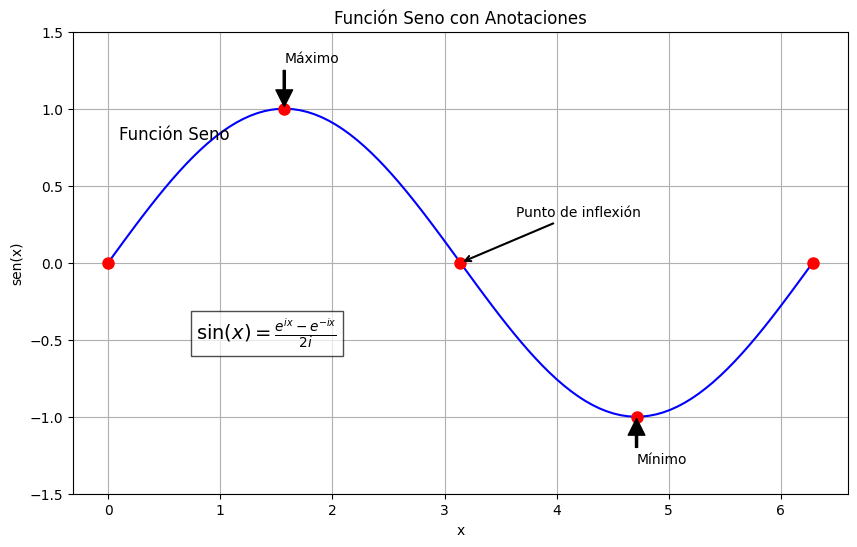
Tipos de Gráficos
Matplotlib proporciona una amplia variedad de tipos de gráficos para diferentes necesidades de visualización. Veamos algunos de los más comunes:
Gráficos de Líneas
Ya hemos visto varios ejemplos de gráficos de líneas, que son ideales para mostrar tendencias a lo largo del tiempo o relaciones continuas:
# Gráfico de líneas con múltiples series
plt.figure(figsize=(10, 6))
# Datos de ejemplo
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x) * np.cos(x)
plt.plot(x, y1, 'b-', label='Seno')
plt.plot(x, y2, 'r--', label='Coseno')
plt.plot(x, y3, 'g-.', label='Seno × Coseno')
plt.title('Gráfico de Líneas Múltiples')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()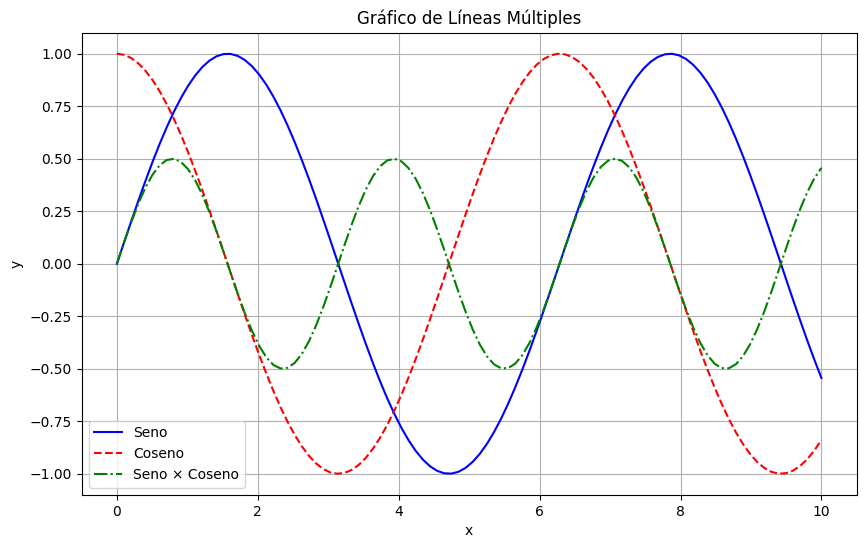
Gráficos de Barras
Los gráficos de barras son perfectos para comparar categorías discretas:
# Gráfico de barras básico
plt.figure(figsize=(10, 6))
# Datos categóricos
categorias = ['A', 'B', 'C', 'D', 'E']
valores = [22, 35, 14, 28, 19]
plt.bar(categorias, valores, color='skyblue', edgecolor='navy')
plt.title('Gráfico de Barras Simple')
plt.xlabel('Categoría')
plt.ylabel('Valor')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
# Gráfico de barras agrupadas
plt.figure(figsize=(10, 6))
# Más datos para comparar
categorias = ['Grupo 1', 'Grupo 2', 'Grupo 3', 'Grupo 4']
hombres = [22, 30, 35, 27]
mujeres = [25, 32, 30, 29]
# Configurar la posición de las barras
x = np.arange(len(categorias))
ancho = 0.35
plt.bar(x - ancho/2, hombres, ancho, label='Hombres', color='cornflowerblue')
plt.bar(x + ancho/2, mujeres, ancho, label='Mujeres', color='lightcoral')
plt.title('Comparación por Género')
plt.xlabel('Grupo')
plt.ylabel('Puntuación')
plt.xticks(x, categorias)
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
# Gráfico de barras apiladas
plt.figure(figsize=(10, 6))
# Datos para barras apiladas
categorias = ['A', 'B', 'C', 'D', 'E']
parte1 = [10, 15, 12, 8, 7]
parte2 = [5, 8, 6, 10, 12]
parte3 = [7, 5, 8, 9, 10]
plt.bar(categorias, parte1, label='Parte 1', color='skyblue')
plt.bar(categorias, parte2, bottom=parte1, label='Parte 2', color='lightgreen')
plt.bar(categorias, parte3, bottom=np.array(parte1) + np.array(parte2),
label='Parte 3', color='salmon')
plt.title('Gráfico de Barras Apiladas')
plt.xlabel('Categoría')
plt.ylabel('Valor')
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
# Gráfico de barras horizontal
plt.figure(figsize=(10, 6))
# Usar los mismos datos
plt.barh(categorias, valores, color='purple', alpha=0.7)
plt.title('Gráfico de Barras Horizontal')
plt.xlabel('Valor')
plt.ylabel('Categoría')
plt.grid(axis='x', linestyle='--', alpha=0.7)
plt.show()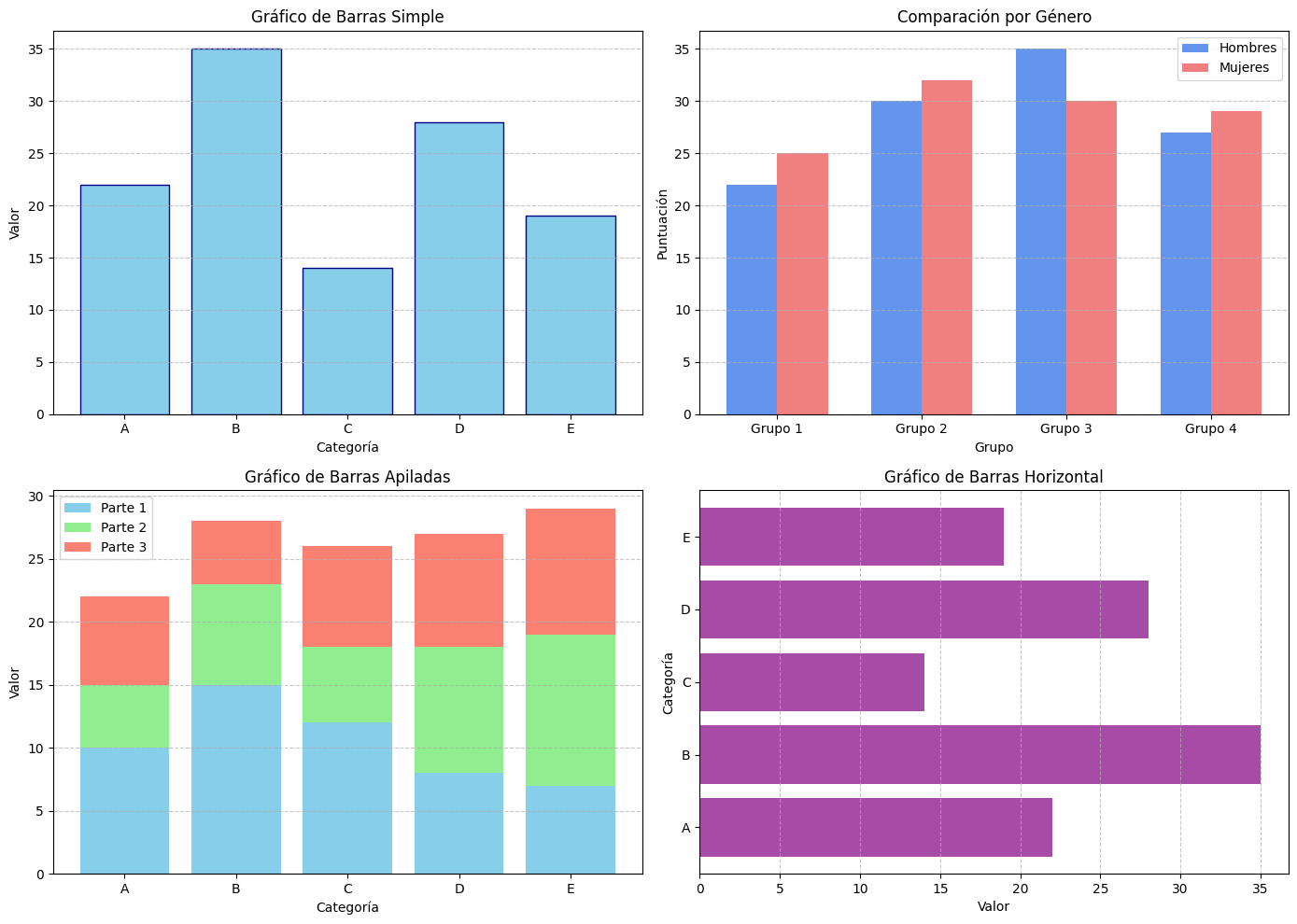
Gráficos de Dispersión (Scatter)
Los gráficos de dispersión son ideales para visualizar relaciones entre dos variables y detectar patrones:
# Gráfico de dispersión básico
plt.figure(figsize=(10, 6))
# Generar datos aleatorios
np.random.seed(42)
x = np.random.rand(50) * 10
y = 2 * x + np.random.randn(50) * 2
# Gráfico de dispersión simple
plt.scatter(x, y, color='blue', alpha=0.7)
plt.title('Gráfico de Dispersión Simple')
plt.xlabel('Variable X')
plt.ylabel('Variable Y')
plt.grid(True)
plt.show()
# Gráfico de dispersión con tamaño y color variables
plt.figure(figsize=(10, 6))
# Más datos aleatorios
np.random.seed(42)
n = 50
x = np.random.rand(n) * 10
y = np.random.rand(n) * 10
colores = np.random.rand(n) # Color basado en valor aleatorio
tamaños = np.random.rand(n) * 500 # Tamaño basado en valor aleatorio
plt.scatter(x, y, c=colores, s=tamaños, alpha=0.7, cmap='viridis')
plt.colorbar(label='Valor Color')
plt.title('Gráfico de Dispersión con Tamaño y Color Variables')
plt.xlabel('Variable X')
plt.ylabel('Variable Y')
plt.grid(True)
plt.show()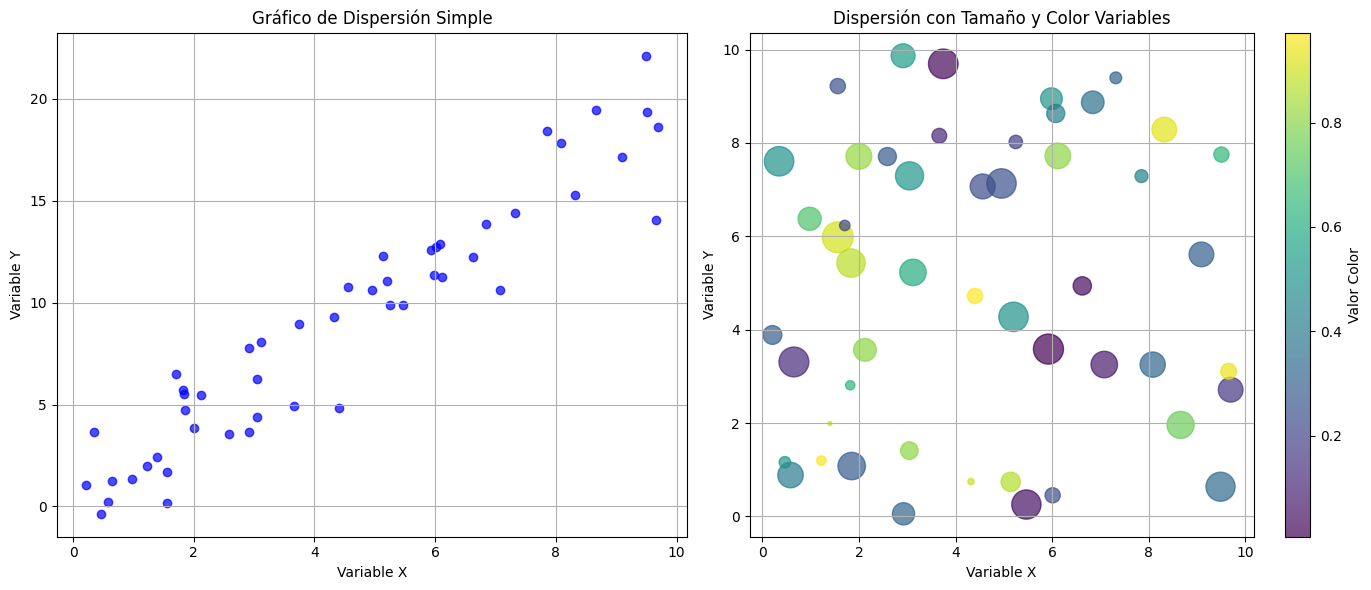
Gráficos Estadísticos Avanzados
Además de los gráficos básicos, Matplotlib ofrece herramientas poderosas para visualizar distribuciones y características estadísticas de los datos. Estos tipos de gráficos son particularmente útiles para el análisis exploratorio de datos.
Histogramas
Los histogramas son perfectos para visualizar la distribución de un conjunto de datos:
# Histograma básico
plt.figure(figsize=(10, 6))
# Generar datos aleatorios con distribución normal
np.random.seed(42)
datos = np.random.normal(loc=0, scale=1, size=1000)
plt.hist(datos, bins=30, color='skyblue', edgecolor='black')
plt.title('Histograma de Distribución Normal')
plt.xlabel('Valor')
plt.ylabel('Frecuencia')
plt.grid(True, alpha=0.3)
plt.show()
# Histograma con múltiples distribuciones
plt.figure(figsize=(10, 6))
# Generar tres distribuciones diferentes
np.random.seed(42)
datos1 = np.random.normal(loc=-2, scale=1, size=1000)
datos2 = np.random.normal(loc=0, scale=1.5, size=1000)
datos3 = np.random.normal(loc=3, scale=2, size=1000)
plt.hist(datos1, bins=30, alpha=0.5, label='Distribución 1')
plt.hist(datos2, bins=30, alpha=0.5, label='Distribución 2')
plt.hist(datos3, bins=30, alpha=0.5, label='Distribución 3')
plt.title('Comparación de Distribuciones')
plt.xlabel('Valor')
plt.ylabel('Frecuencia')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()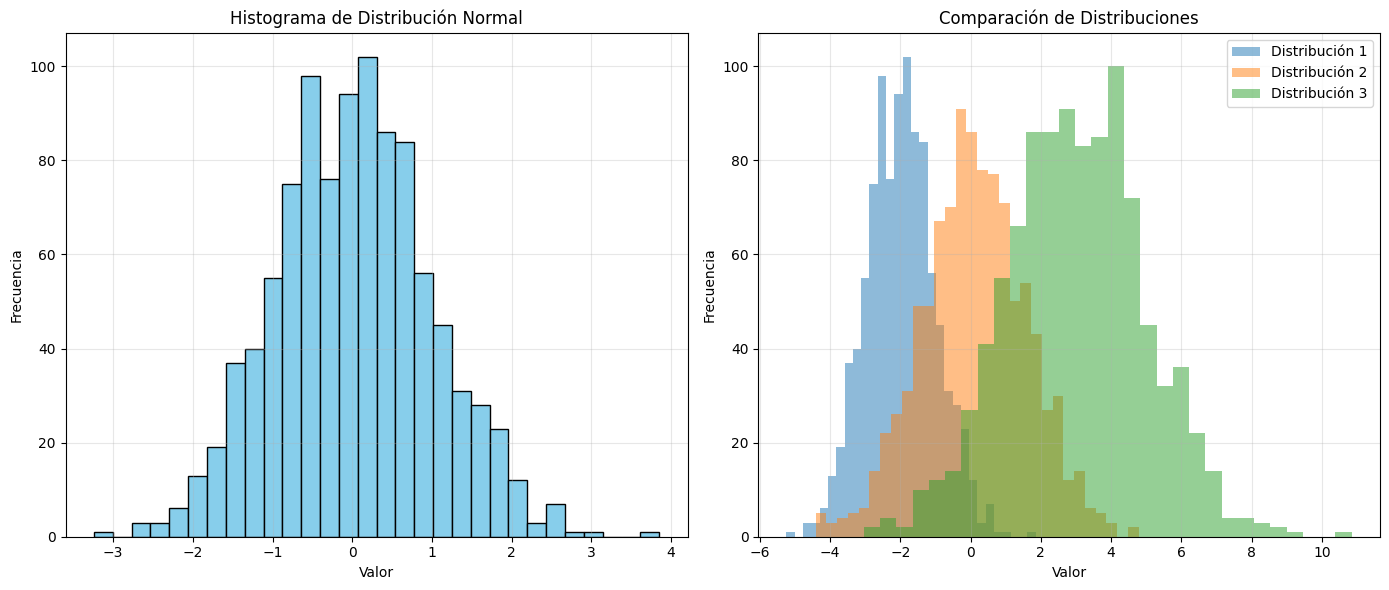
Diagramas de Caja (Boxplot)
Los diagramas de caja o boxplots son ideales para visualizar la distribución de datos, mostrando estadísticas clave como la mediana, cuartiles y valores atípicos:
# Boxplot básico
plt.figure(figsize=(10, 6))
# Generar datos aleatorios
np.random.seed(42)
datos = [np.random.normal(0, std, 100) for std in range(1, 5)]
# Crear boxplot
plt.boxplot(datos)
plt.title('Boxplot Simple')
plt.xlabel('Grupo')
plt.ylabel('Valor')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
# Boxplot personalizado con colores
plt.figure(figsize=(10, 6))
# Crear boxplot con más opciones
bplot = plt.boxplot(datos,
patch_artist=True, # Rellenar las cajas con color
labels=['Grupo 1', 'Grupo 2', 'Grupo 3', 'Grupo 4'],
showmeans=True, # Mostrar la media
meanline=True) # Mostrar la media como línea
# Colores para las cajas
colores = ['lightblue', 'lightgreen', 'tan', 'pink']
for patch, color in zip(bplot['boxes'], colores):
patch.set_facecolor(color)
# Personalizar otros elementos
for element in ['whiskers', 'fliers', 'means', 'medians', 'caps']:
plt.setp(bplot[element], color='black')
plt.title('Boxplot Personalizado')
plt.xlabel('Grupo')
plt.ylabel('Valor')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()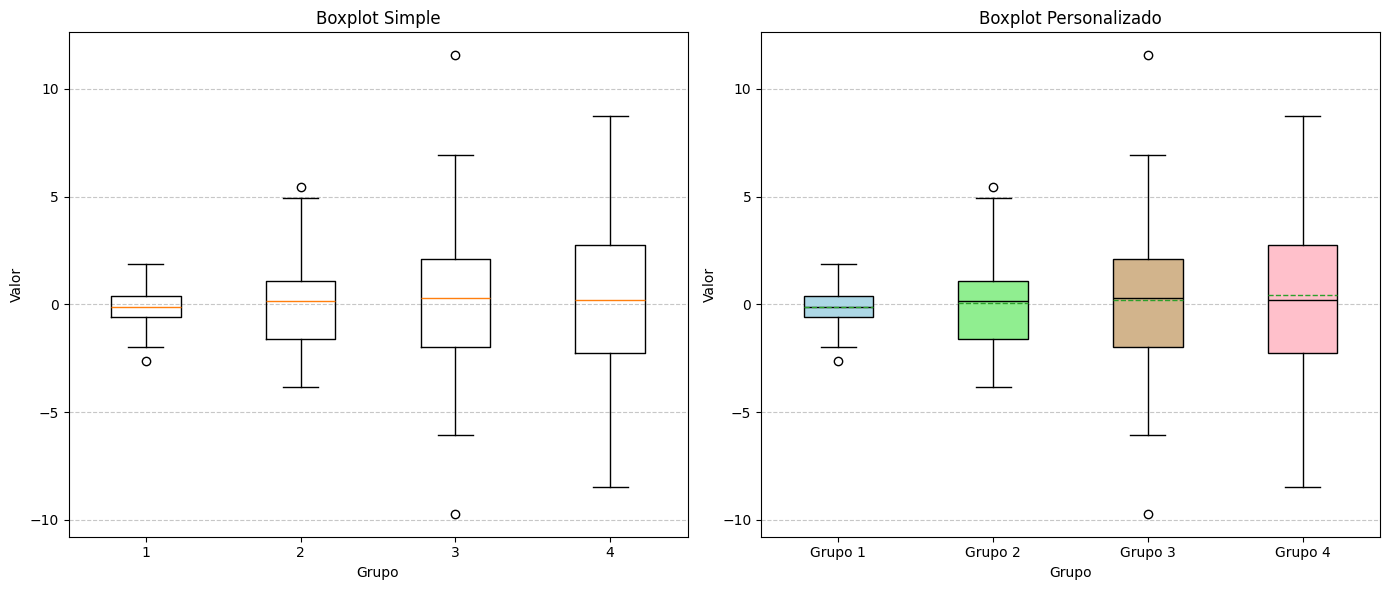
Diagramas de Violín
Los diagramas de violín combinan características de los boxplots con estimaciones de densidad, proporcionando una visualización más completa de la distribución:
# Diagrama de violín básico
plt.figure(figsize=(10, 6))
# Usar los mismos datos del boxplot
plt.violinplot(datos)
plt.title('Diagrama de Violín Simple')
plt.xlabel('Grupo')
plt.ylabel('Valor')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.xticks([1, 2, 3, 4], ['Grupo 1', 'Grupo 2', 'Grupo 3', 'Grupo 4'])
plt.show()
# Comparación de boxplot y violinplot
plt.figure(figsize=(12, 6))
# Crear un layout con dos subplots
plt.subplot(1, 2, 1)
plt.boxplot(datos)
plt.title('Boxplot')
plt.xlabel('Grupo')
plt.ylabel('Valor')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.xticks([1, 2, 3, 4], ['Grupo 1', 'Grupo 2', 'Grupo 3', 'Grupo 4'])
plt.subplot(1, 2, 2)
plt.violinplot(datos)
plt.title('Diagrama de Violín')
plt.xlabel('Grupo')
plt.ylabel('Valor')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.xticks([1, 2, 3, 4], ['Grupo 1', 'Grupo 2', 'Grupo 3', 'Grupo 4'])
plt.tight_layout()
plt.show()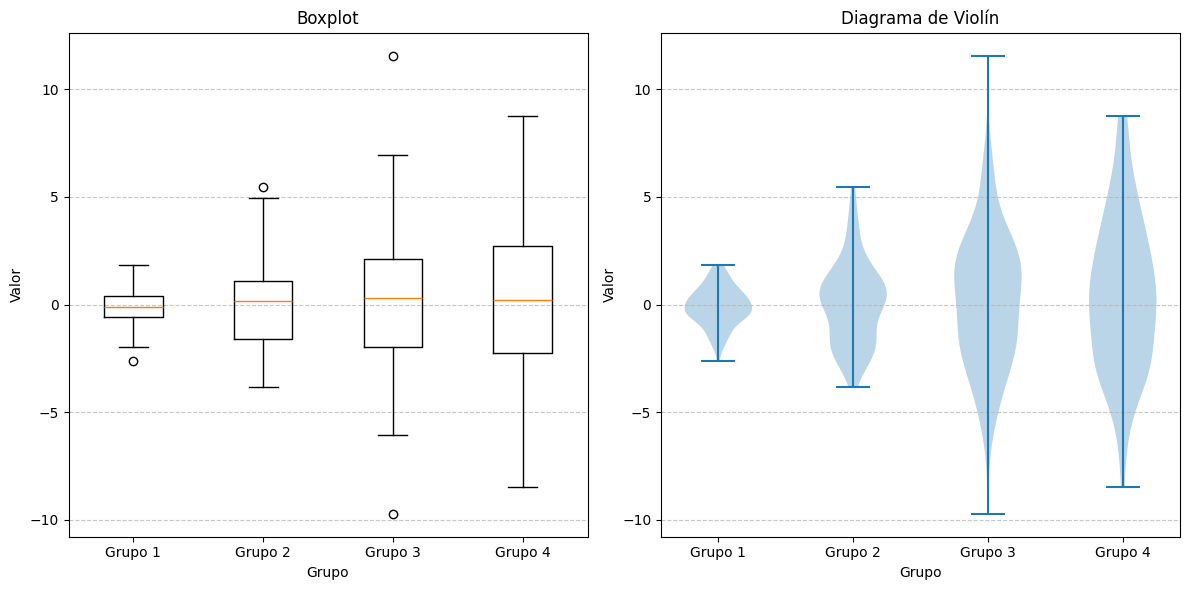
Diagramas de Torta (Pie Charts)
Los diagramas de torta son útiles para mostrar la composición proporcional de un conjunto de datos:
# Diagrama de torta básico
plt.figure(figsize=(8, 8))
# Datos para el diagrama
categorias = ['A', 'B', 'C', 'D', 'E']
valores = [35, 25, 20, 15, 5]
# Crear diagrama de torta
plt.pie(valores,
labels=categorias,
autopct='%1.1f%%', # Mostrar porcentajes con 1 decimal
startangle=90) # Ángulo de inicio (0 grados en el eje x)
plt.title('Diagrama de Torta Simple')
plt.axis('equal') # Asegurar que el gráfico sea circular
plt.show()
# Diagrama de torta personalizado
plt.figure(figsize=(10, 8))
# Datos para el diagrama
categorias = ['Categoría A', 'Categoría B', 'Categoría C', 'Categoría D', 'Otros']
valores = [38, 27, 19, 10, 6]
colores = ['#ff9999', '#66b3ff', '#99ff99', '#ffcc99', '#c2c2f0']
explode = (0.1, 0, 0, 0, 0) # Destacar la primera rebanada
# Crear diagrama de torta personalizado
plt.pie(valores,
labels=categorias,
autopct='%1.1f%%',
startangle=90,
shadow=True, # Añadir sombra
explode=explode, # Destacar rebanadas
colors=colores) # Colores personalizados
plt.title('Distribución por Categorías', size=14)
plt.axis('equal')
# Añadir leyenda
plt.legend(categorias, loc='best', bbox_to_anchor=(1, 0.5))
plt.tight_layout()
plt.show()
# Diagrama de dona (torta con un círculo en el centro)
plt.figure(figsize=(10, 8))
# Crear diagrama de torta
plt.pie(valores,
labels=categorias,
autopct='%1.1f%%',
startangle=90,
colors=colores)
# Añadir un círculo en el centro para crear efecto de dona
centro_circulo = plt.Circle((0,0), 0.7, fc='white')
fig = plt.gcf()
fig.gca().add_artist(centro_circulo)
# Añadir texto en el centro
plt.text(0, 0, 'Total:\n100', ha='center', va='center', fontsize=20)
plt.title('Diagrama de Dona')
plt.axis('equal')
plt.tight_layout()
plt.show()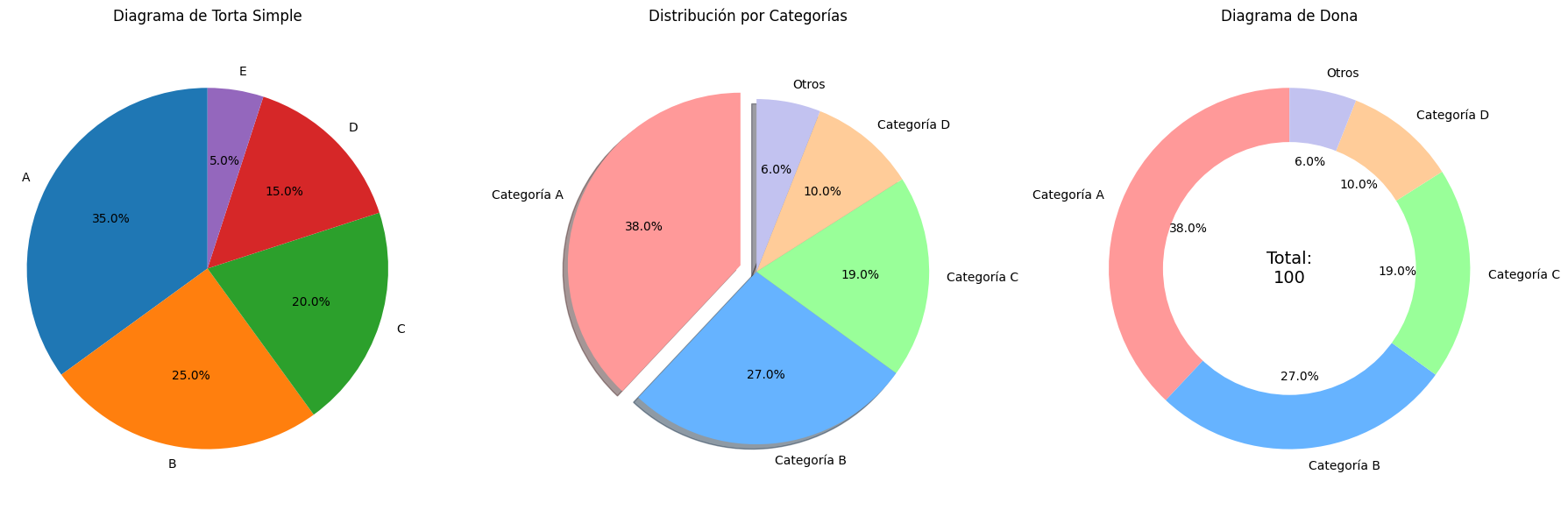
Diagramas de Error
Los diagramas de error son esenciales para mostrar la incertidumbre o variabilidad en un conjunto de datos:
# Diagramas de error básicos
plt.figure(figsize=(10, 6))
# Datos para el gráfico
x = np.arange(1, 6)
y = np.array([5, 7, 4, 6, 8])
error = np.array([0.8, 1.2, 0.5, 1.0, 0.9])
# Gráfico de barras con barras de error
plt.bar(x, y, yerr=error, align='center', alpha=0.7, capsize=10,
color='skyblue', ecolor='black')
plt.xlabel('Categoría')
plt.ylabel('Valor')
plt.title('Gráfico de Barras con Barras de Error')
plt.xticks(x, ['A', 'B', 'C', 'D', 'E'])
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
# Gráfico de líneas con barras de error
plt.figure(figsize=(10, 6))
# Datos para el gráfico
x = np.arange(0, 10, 1)
y = np.exp(-x/10.0) * np.cos(x)
error = 0.1 + 0.1 * np.sqrt(x)
# Gráfico de líneas con barras de error
plt.errorbar(x, y, yerr=error, fmt='o-', capsize=5, capthick=1,
ecolor='red', markerfacecolor='blue', markersize=8)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Gráfico de Líneas con Barras de Error')
plt.grid(True)
plt.show()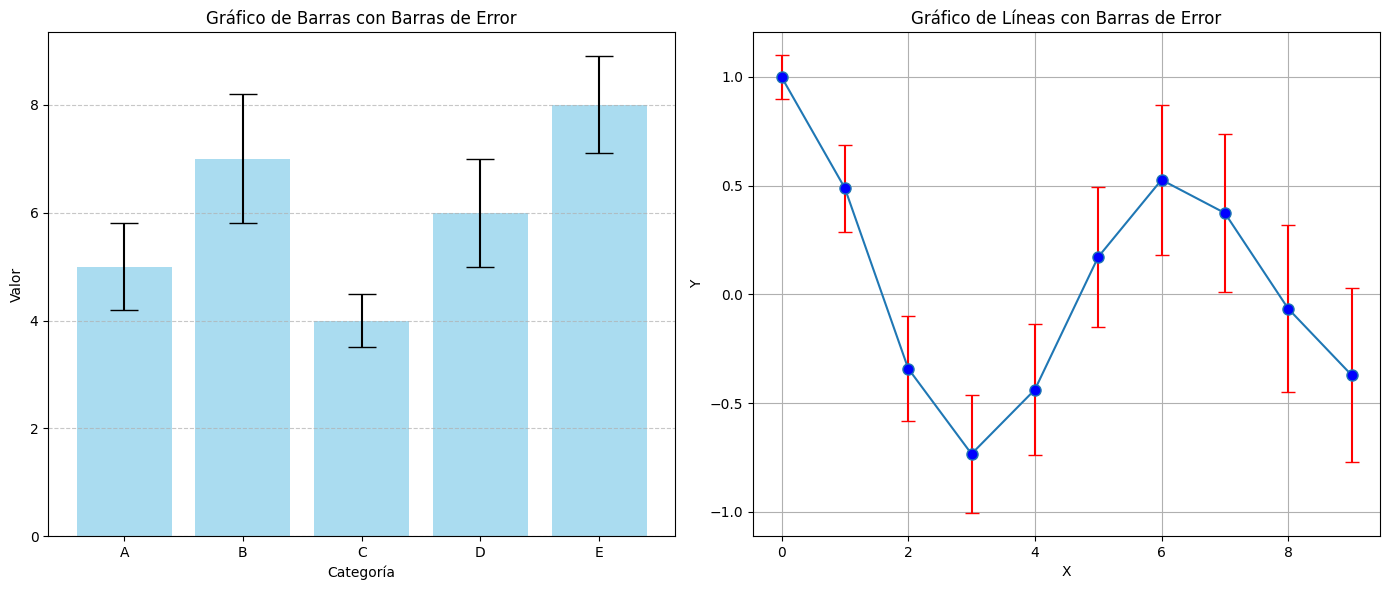
Material de Práctica
Para consolidar tu conocimiento sobre visualización de datos con Matplotlib, aquí tienes algunos notebooks interactivos y ejercicios prácticos:
- Ejercicios de visualización de datos - Pon a prueba tus habilidades con este ejercicio práctico.
- Exploración de datos con visualización - Utiliza Matplotlib para explorar datasets reales.
Referencias
Para profundizar tus conocimientos sobre visualización de datos en Python, te recomendamos estos recursos:
- Galería de Matplotlib - Una extensa colección de ejemplos con código para diferentes tipos de visualizaciones.
- Tutoriales oficiales de Matplotlib - Guías detalladas para aprender a utilizar todas las funcionalidades de la biblioteca.
- Python Plot - Una guía interactiva que compara diferentes bibliotecas de visualización en Python con ejemplos prácticos.
- Scientific Visualization: Python + Matplotlib - Un libro gratuito de Nicolas P. Rougier que cubre visualización científica avanzada.
- Tutoriales de Seaborn - Aunque nos hemos centrado en Matplotlib, Seaborn es una biblioteca construida sobre Matplotlib que simplifica la creación de visualizaciones estadísticas complejas.