Capítulo 9: Algoritmos de Clustering
¿Qué es el Clustering?
El clustering es una técnica de aprendizaje no supervisado que agrupa datos similares en conjuntos llamados clusters. A diferencia del aprendizaje supervisado, el clustering no requiere datos etiquetados y busca patrones intrínsecos en los datos para identificar grupos naturales.
Comparación visual de diferentes algoritmos de clustering en conjuntos de datos simulados (Fuente: Scikit-learn)
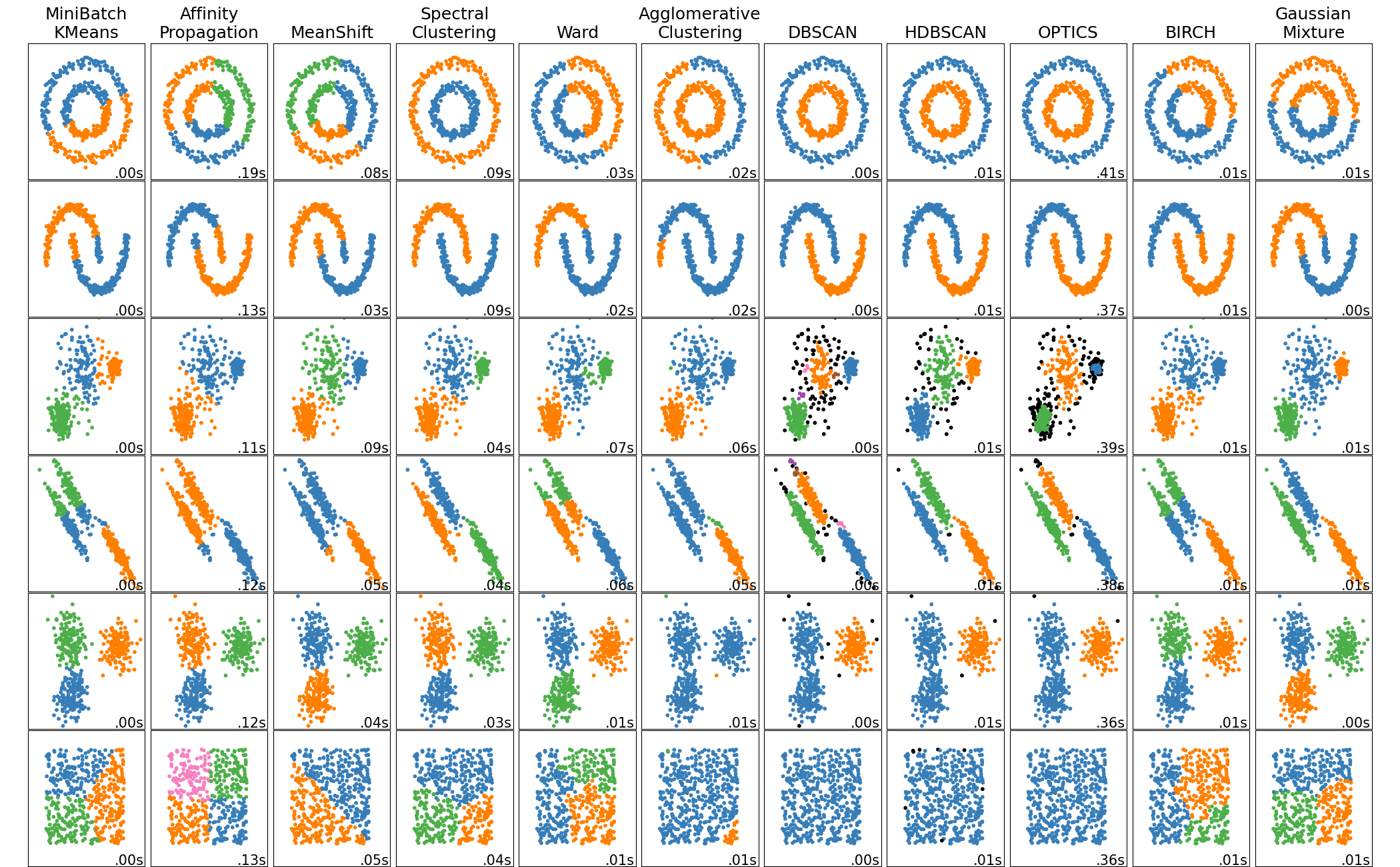
El clustering se utiliza en numerosos campos y aplicaciones:
- Marketing: Segmentación de clientes basada en comportamiento de compra
- Biología: Agrupación de genes con expresión similar
- Astronomía: Clasificación de estrellas y galaxias
- Medicina: Identificación de subtipos de enfermedades
- Análisis de documentos: Organización temática de textos
- Detección de anomalías: Identificación de patrones atípicos
Principales Técnicas de Clustering
Existen varios enfoques para el clustering, cada uno con sus propias fortalezas y características:
Clustering Basado en Centroides
Los algoritmos basados en centroides dividen los datos en K grupos, donde cada grupo está representado por un punto central llamado centroide.
El algoritmo más conocido es K-means, que:
- Asigna cada punto al centroide más cercano
- Recalcula los centroides como el promedio de los puntos asignados
- Repite el proceso hasta la convergencia
Clustering Jerárquico
El clustering jerárquico crea una descomposición anidada de los datos, formando un árbol de clusters (dendrograma).
Existen dos enfoques principales:
- Aglomerativo: Comienza con cada punto como un cluster y los fusiona gradualmente
- Divisivo: Comienza con un solo cluster y lo divide recursivamente
Clustering Basado en Densidad
Los algoritmos basados en densidad identifican regiones densas de puntos separadas por regiones de baja densidad.
El algoritmo más popular es DBSCAN (Density-Based Spatial Clustering of Applications with Noise), que:
- Define clusters como áreas densas conectadas
- Puede detectar clusters de forma arbitraria
- Identifica automáticamente puntos de ruido o valores atípicos
A diferencia de la clasificación y regresión, en el clustering no hay una "respuesta correcta" predefinida. La evaluación de los resultados a menudo requiere métricas internas (como cohesión y separación) o validación basada en conocimiento del dominio.
Workflow Completo de Clustering: Análisis del Dataset Iris
A continuación, implementaremos un flujo de trabajo completo de clustering utilizando el famoso dataset Iris. Este ejercicio práctico te permitirá experimentar con diferentes algoritmos de clustering, comparar su rendimiento y optimizar hiperparámetros.
Nuestro objetivo es:
- Implementar algoritmos de clustering (KMeans, Agglomerative, DBSCAN, MeanShift)
- Comparar rendimiento usando métricas de evaluación
- Optimizar hiperparámetros usando PCA para reducción dimensional
1. Importación de Librerías
Comenzamos importando todas las librerías necesarias para nuestro análisis de clustering:
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import warnings
warnings.filterwarnings("ignore")
# Librerías de sklearn
from sklearn import metrics
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN, MeanShift
from sklearn import preprocessing
from sklearn.decomposition import PCA
from sklearn.model_selection import ParameterGrid
# Configuración de gráficos
plt.style.use('default')
plt.rcParams['figure.figsize'] = (10, 6)2. Carga y Exploración del Dataset Iris
El dataset Iris es perfecto para practicar clustering ya que contiene 150 muestras de flores con 4 características numéricas y 3 clases naturales (especies). Aunque conocemos las etiquetas verdaderas, las usaremos solo para evaluar qué tan bien nuestros algoritmos de clustering descubren los grupos naturales.
# Cargar el dataset Iris desde sklearn
from sklearn.datasets import load_iris
# Cargar datos
iris_data = load_iris()
iris_df = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
iris_df['class'] = iris_data.target
# Renombrar columnas para mayor claridad
iris_df.columns = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
print("Forma del dataset:", iris_df.shape)
print("\nPrimeras 5 filas:")
iris_df.head()Forma del dataset: (150, 5)
Primeras 5 filas:
sepal-length sepal-width petal-length petal-width class
0 5.1 3.5 1.4 0.2 0
1 4.9 3.0 1.4 0.2 0
2 4.7 3.2 1.3 0.2 0
3 4.6 3.1 1.5 0.2 0
4 5.0 3.6 1.4 0.2 0Examinemos las características básicas del dataset:
# Información básica del dataset
print("Información del dataset:")
print("\nClases únicas:", iris_df['class'].unique())
print("Distribución de clases:")
print(iris_df['class'].value_counts().sort_index())
print("\nVerificar valores nulos:")
print(iris_df.isnull().sum())
print("\nEstadísticas descriptivas:")
iris_df.describe()Información del dataset:
Clases únicas: [0 1 2]
Distribución de clases:
class
0 50
1 50
2 50
Name: count, dtype: int64
Verificar valores nulos:
sepal-length 0
sepal-width 0
petal-length 0
petal-width 0
class 0
dtype: int643. Preprocesamiento de Datos
Antes de aplicar los algoritmos de clustering, preparamos los datos mezclando el dataset aleatoriamente y separando las características de las etiquetas:
# Mezclar el dataset aleatoriamente
iris_df = iris_df.sample(frac=1, random_state=42).reset_index(drop=True)
print("Dataset después de mezclar:")
print(iris_df.head())
# Separar características y etiquetas
iris_features = iris_df.drop('class', axis=1)
iris_labels = iris_df['class']
print(f"\nForma de características: {iris_features.shape}")
print(f"Forma de etiquetas: {iris_labels.shape}")Dataset después de mezclar:
sepal-length sepal-width petal-length petal-width class
0 6.1 2.8 4.7 1.2 1
1 5.7 3.8 1.7 0.3 0
2 7.7 2.6 6.9 2.3 2
3 6.0 2.9 4.5 1.5 1
4 6.8 2.8 4.8 1.4 1
Forma de características: (150, 4)
Forma de etiquetas: (150,)4. Análisis Exploratorio de Datos
4.1 Análisis Univariable
Comenzamos explorando las distribuciones individuales de cada característica para entender mejor nuestros datos:
# Análisis univariable - Estadísticas por característica
print("Estadísticas descriptivas de las características:")
iris_features.describe()# Visualizar distribuciones
fig, axes = plt.subplots(2, 2, figsize=(8, 6))
axes = axes.ravel()
for i, column in enumerate(iris_features.columns):
axes[i].hist(iris_features[column], bins=20, alpha=0.7, color='skyblue', edgecolor='black')
axes[i].set_title(f'Distribución de {column}')
axes[i].set_xlabel(column)
axes[i].set_ylabel('Frecuencia')
plt.tight_layout()
plt.show()
Distribuciones de las cuatro características principales del dataset Iris
4.2 Análisis Bivariable
Exploramos las relaciones entre pares de características mediante scatter plots para identificar posibles patrones de agrupamiento:
# Análisis bivariable - Scatter plots
fig, axes = plt.subplots(2, 2, figsize=(8, 6))
# Scatter plot 1: sepal-length vs sepal-width
axes[0,0].scatter(iris_df['sepal-length'], iris_df['sepal-width'], cmap='viridis', s=60, alpha=0.7)
axes[0,0].set_xlabel('Sepal Length')
axes[0,0].set_ylabel('Sepal Width')
axes[0,0].set_title('Sepal Length vs Sepal Width')
# Scatter plot 2: petal-length vs petal-width
axes[0,1].scatter(iris_df['petal-length'], iris_df['petal-width'], cmap='viridis', s=60, alpha=0.7)
axes[0,1].set_xlabel('Petal Length')
axes[0,1].set_ylabel('Petal Width')
axes[0,1].set_title('Petal Length vs Petal Width')
# Scatter plot 3: sepal-length vs petal-length
axes[1,0].scatter(iris_df['sepal-length'], iris_df['petal-length'], cmap='viridis', s=60, alpha=0.7)
axes[1,0].set_xlabel('Sepal Length')
axes[1,0].set_ylabel('Petal Length')
axes[1,0].set_title('Sepal Length vs Petal Length')
# Scatter plot 4: sepal-width vs petal-width
axes[1,1].scatter(iris_df['sepal-width'], iris_df['petal-width'], cmap='viridis', s=60, alpha=0.7)
axes[1,1].set_xlabel('Sepal Width')
axes[1,1].set_ylabel('Petal Width')
axes[1,1].set_title('Sepal Width vs Petal Width')
plt.tight_layout()
plt.show()
Relaciones entre pares de características mostrando patrones de agrupamiento natural
Calculamos la matriz de correlación para entender mejor las relaciones lineales entre las variables:
# Matriz de correlación
correlation_matrix = iris_features.corr()
# Visualizar matriz de correlación
plt.figure(figsize=(8, 6))
plt.imshow(correlation_matrix, cmap='coolwarm', aspect='auto')
plt.colorbar()
plt.xticks(range(len(correlation_matrix.columns)), correlation_matrix.columns, rotation=45)
plt.yticks(range(len(correlation_matrix.columns)), correlation_matrix.columns)
plt.title('Matriz de Correlación - Dataset Iris')
# Añadir valores numéricos
for i in range(len(correlation_matrix.columns)):
for j in range(len(correlation_matrix.columns)):
plt.text(j, i, f'{correlation_matrix.iloc[i, j]:.2f}',
ha='center', va='center', color='black')
plt.tight_layout()
plt.show()
Matriz de correlación mostrando las relaciones lineales entre características
5. Implementación de K-Means
Comenzamos con K-Means, uno de los algoritmos de clustering más populares. Aplicamos el algoritmo usando todas las características del dataset y evaluamos su rendimiento:
# Implementar KMeans con todas las características
kmeans_model = KMeans(n_clusters=3, random_state=42, max_iter=1000).fit(iris_features)
# Obtener las etiquetas predichas y centroides
predicted_labels = kmeans_model.labels_
centroids = kmeans_model.cluster_centers_
print("Centroides de los clusters:")
print(pd.DataFrame(centroids, columns=iris_features.columns))
print(f"\nNúmero de puntos por cluster:")
unique, counts = np.unique(predicted_labels, return_counts=True)
for i, count in enumerate(counts):
print(f"Cluster {i}: {count} puntos")Centroides de los clusters:
sepal-length sepal-width petal-length petal-width
0 5.006000 3.428000 1.462000 0.246000
1 5.901613 2.748387 4.393548 1.433871
2 6.850000 3.073684 5.742105 2.071053
Número de puntos por cluster:
Cluster 0: 50 puntos
Cluster 1: 62 puntos
Cluster 2: 38 puntosPara evaluar la calidad del clustering, definimos una función que calcula múltiples métricas de evaluación:
# Función para calcular métricas de evaluación
def evaluate_clustering(true_labels, predicted_labels, data):
"""
Calcula las métricas de evaluación para clustering
"""
silhouette = metrics.silhouette_score(data, predicted_labels)
adjusted_rand = metrics.adjusted_rand_score(true_labels, predicted_labels)
homogeneity = metrics.homogeneity_score(true_labels, predicted_labels)
return {
'Silhouette Score': silhouette,
'Adjusted Rand Score': adjusted_rand,
'Homogeneity Score': homogeneity
}
# Evaluar KMeans
kmeans_metrics = evaluate_clustering(iris_labels, predicted_labels, iris_features)
print("Métricas de evaluación para KMeans:")
print("-" * 40)
for metric, value in kmeans_metrics.items():
print(f"{metric}: {value:.4f}")Métricas de evaluación para KMeans:
----------------------------------------
Silhouette Score: 0.5528
Adjusted Rand Score: 0.7302
Homogeneity Score: 0.7515Visualizamos los resultados comparando el clustering real con el predicho por K-Means:
# Visualizar resultados de KMeans
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
# Gráfico 1: Clustering real vs predicho
axes[0].scatter(iris_features['sepal-length'], iris_features['petal-length'],
c=iris_labels, cmap='viridis', s=40, alpha=0.7, edgecolors='black')
axes[0].set_title('Clustering Real (Ground Truth)')
axes[0].set_xlabel('Sepal Length')
axes[0].set_ylabel('Petal Length')
axes[1].scatter(iris_features['sepal-length'], iris_features['petal-length'],
c=predicted_labels, cmap='viridis', s=40, alpha=0.7, edgecolors='black')
axes[1].scatter(centroids[:, 0], centroids[:, 2], c='red', s=50, marker='X',
edgecolors='black', label='Centroides')
axes[1].set_title('Clustering KMeans')
axes[1].set_xlabel('Sepal Length')
axes[1].set_ylabel('Petal Length')
axes[1].legend()
plt.tight_layout()
plt.show()
Comparación entre las clases reales del dataset Iris y los clusters encontrados por K-Means
6. Comparación de Algoritmos de Clustering
Ahora compararemos el rendimiento de diferentes algoritmos de clustering para determinar cuál funciona mejor con nuestros datos. Implementaremos K-Means, Clustering Aglomerativo, DBSCAN y MeanShift:
# Función para construir y evaluar modelos
def build_and_evaluate_model(clustering_function, data, true_labels, **kwargs):
"""
Construye un modelo de clustering y evalúa su rendimiento
"""
model = clustering_function(**kwargs).fit(data)
metrics_dict = evaluate_clustering(true_labels, model.labels_, data)
return model, metrics_dict
# Diccionario para almacenar resultados
results = {}
models = {}
print("Evaluando algoritmos de clustering...")
print("=" * 60)Evaluando algoritmos de clustering...
============================================================6.1 K-Means
# 1. KMeans
print("1. KMeans")
print("-" * 20)
kmeans_model, kmeans_results = build_and_evaluate_model(
KMeans, iris_features, iris_labels,
n_clusters=3, max_iter=1000
)
results['KMeans'] = kmeans_results
models['KMeans'] = kmeans_model
for metric, value in kmeans_results.items():
print(f"{metric}: {value:.4f}")
print()1. KMeans
--------------------
Silhouette Score: 0.5512
Adjusted Rand Score: 0.7163
Homogeneity Score: 0.73646.2 Clustering Aglomerativo
# 2. Agglomerative Clustering
print("2. Agglomerative Clustering")
print("-" * 30)
agg_model, agg_results = build_and_evaluate_model(
AgglomerativeClustering, iris_features, iris_labels,
n_clusters=3
)
results['Agglomerative'] = agg_results
models['Agglomerative'] = agg_model
for metric, value in agg_results.items():
print(f"{metric}: {value:.4f}")
print()2. Agglomerative Clustering
------------------------------
Silhouette Score: 0.5543
Adjusted Rand Score: 0.7312
Homogeneity Score: 0.76086.3 DBSCAN
# 3. DBSCAN
print("3. DBSCAN")
print("-" * 15)
dbscan_model, dbscan_results = build_and_evaluate_model(
DBSCAN, iris_features, iris_labels,
eps=0.9, min_samples=5
)
results['DBSCAN'] = dbscan_results
models['DBSCAN'] = dbscan_model
for metric, value in dbscan_results.items():
print(f"{metric}: {value:.4f}")
# Información adicional sobre DBSCAN
n_clusters = len(set(dbscan_model.labels_)) - (1 if -1 in dbscan_model.labels_ else 0)
n_noise = list(dbscan_model.labels_).count(-1)
print(f"Número de clusters encontrados: {n_clusters}")
print(f"Puntos de ruido: {n_noise}")
print()3. DBSCAN
---------------
Silhouette Score: 0.6867
Adjusted Rand Score: 0.5681
Homogeneity Score: 0.5794
Número de clusters encontrados: 2
Puntos de ruido: 06.4 MeanShift
# 4. MeanShift
print("4. MeanShift")
print("-" * 15)
from sklearn.cluster import estimate_bandwidth
# Estimar bandwidth automáticamente
bandwidth = estimate_bandwidth(iris_features)
print(f"Bandwidth estimado: {bandwidth:.4f}")
meanshift_model, meanshift_results = build_and_evaluate_model(
MeanShift, iris_features, iris_labels,
bandwidth=bandwidth
)
results['MeanShift'] = meanshift_results
models['MeanShift'] = meanshift_model
for metric, value in meanshift_results.items():
print(f"{metric}: {value:.4f}")
n_clusters_ms = len(set(meanshift_model.labels_))
print(f"Número de clusters encontrados: {n_clusters_ms}")4. MeanShift
---------------
Bandwidth estimado: 1.2021
Silhouette Score: 0.6858
Adjusted Rand Score: 0.5584
Homogeneity Score: 0.5537
Número de clusters encontrados: 26.5 Resumen Comparativo
# Crear tabla comparativa de resultados
results_df = pd.DataFrame(results).T
results_df = results_df.round(4)
print("RESUMEN COMPARATIVO DE ALGORITMOS")
print("=" * 50)
print(results_df)RESUMEN COMPARATIVO DE ALGORITMOS
==================================================
Silhouette Score Adjusted Rand Score Homogeneity Score
KMeans 0.5512 0.7163 0.7364
Agglomerative 0.5543 0.7312 0.7608
DBSCAN 0.6867 0.5681 0.5794
MeanShift 0.6858 0.5584 0.5537# Visualizar comparación
fig, axes = plt.subplots(1, 3, figsize=(14, 5))
metrics_names = list(results_df.columns)
for i, metric in enumerate(metrics_names):
algorithms = results_df.index
values = results_df[metric]
bars = axes[i].bar(algorithms, values, color=['skyblue', 'lightgreen', 'salmon', 'gold'])
axes[i].set_title(f'{metric}')
axes[i].set_ylabel('Score')
axes[i].tick_params(axis='x', rotation=45)
# Añadir valores en las barras
for bar, value in zip(bars, values):
height = bar.get_height()
axes[i].text(bar.get_x() + bar.get_width()/2., height + 0.01,
f'{value:.3f}', ha='center', va='bottom')
plt.tight_layout()
plt.show()
Comparación visual de las métricas de evaluación para todos los algoritmos de clustering
7. Optimización de Hiperparámetros usando PCA
Para mejorar nuestros resultados y facilitar la visualización, aplicamos PCA (Análisis de Componentes Principales) para reducir la dimensionalidad a 2 componentes, manteniendo la mayor parte de la varianza de los datos originales:
# Aplicar PCA para reducir a 2 componentes
pca = PCA(n_components=2, random_state=42)
iris_pca = pca.fit_transform(iris_features)
print("Varianza explicada por cada componente:")
for i, variance in enumerate(pca.explained_variance_ratio_):
print(f"Componente {i+1}: {variance:.4f} ({variance*100:.2f}%)")
print(f"\nVarianza total explicada: {sum(pca.explained_variance_ratio_):.4f} ({sum(pca.explained_variance_ratio_)*100:.2f}%)")
# Crear DataFrame con componentes PCA
iris_pca_df = pd.DataFrame(iris_pca, columns=['PC1', 'PC2'])
iris_pca_df['class'] = iris_labels.values
print(f"\nForma de datos después de PCA: {iris_pca_df.shape}")
iris_pca_df.head()Varianza explicada por cada componente:
Componente 1: 0.9246 (92.46%)
Componente 2: 0.0531 (5.31%)
Varianza total explicada: 0.9777 (97.77%)
Forma de datos después de PCA: (150, 3)# Visualizar datos después de PCA
plt.figure(figsize=(10, 6))
scatter = plt.scatter(iris_pca_df['PC1'], iris_pca_df['PC2'],
c=iris_pca_df['class'], cmap='viridis', s=70, alpha=0.7, edgecolors='black')
plt.xlabel(f'Primera Componente Principal')
plt.ylabel(f'Segunda Componente Principal')
plt.title('Dataset Iris después de PCA (2 componentes)')
plt.grid(True, alpha=0.3)
plt.show()
# Datos para optimización
pca_features = iris_pca_df[['PC1', 'PC2']]
Dataset Iris proyectado en un espacio bidimensional usando PCA, conservando 97.77% de la varianza
7.1 Optimización de K-Means
Ahora optimizamos los hiperparámetros de cada algoritmo utilizando los datos transformados por PCA:
# Optimización de hiperparámetros para KMeans
print("OPTIMIZACIÓN DE HIPERPARÁMETROS - KMEANS")
print("=" * 50)
# Parámetros a probar
kmeans_params = {'n_clusters': [2, 3, 4, 5]}
parameter_grid = ParameterGrid(kmeans_params)
best_kmeans_score = -1
best_kmeans_params = None
kmeans_results_opt = []
for params in parameter_grid:
model = KMeans(random_state=42, max_iter=1000, **params)
model.fit(pca_features)
silhouette = metrics.silhouette_score(pca_features, model.labels_)
result = {'params': params, 'silhouette_score': silhouette}
kmeans_results_opt.append(result)
print(f"Parámetros: {params} | Silhouette Score: {silhouette:.4f}")
if silhouette > best_kmeans_score:
best_kmeans_score = silhouette
best_kmeans_params = params
print(f"\nMejores parámetros KMeans: {best_kmeans_params}")
print(f"Mejor Silhouette Score: {best_kmeans_score:.4f}")OPTIMIZACIÓN DE HIPERPARÁMETROS - KMEANS
==================================================
Parámetros: {'n_clusters': 2} | Silhouette Score: 0.6810
Parámetros: {'n_clusters': 3} | Silhouette Score: 0.5528
Parámetros: {'n_clusters': 4} | Silhouette Score: 0.4979
Parámetros: {'n_clusters': 5} | Silhouette Score: 0.4258
Mejores parámetros KMeans: {'n_clusters': 2}
Mejor Silhouette Score: 0.68107.2 Optimización de DBSCAN
# Optimización de hiperparámetros para DBSCAN
print("\nOPTIMIZACIÓN DE HIPERPARÁMETROS - DBSCAN")
print("=" * 50)
# Parámetros a probar
dbscan_params = {
'eps': [0.3, 0.5, 0.7, 0.9],
'min_samples': [3, 5, 7]
}
parameter_grid = ParameterGrid(dbscan_params)
best_dbscan_score = -1
best_dbscan_params = None
dbscan_results_opt = []
for params in parameter_grid:
model = DBSCAN(**params)
model.fit(pca_features)
# Verificar que se formaron clusters válidos
n_clusters = len(set(model.labels_)) - (1 if -1 in model.labels_ else 0)
n_noise = list(model.labels_).count(-1)
silhouette = metrics.silhouette_score(pca_features, model.labels_)
result = {'params': params, 'silhouette_score': silhouette,
'n_clusters': n_clusters, 'n_noise': n_noise}
dbscan_results_opt.append(result)
print(f"Parámetros: {params} | Silhouette: {silhouette:.4f} | Clusters: {n_clusters} | Ruido: {n_noise}")
if silhouette > best_dbscan_score:
best_dbscan_score = silhouette
best_dbscan_params = params
print(f"\nMejores parámetros DBSCAN: {best_dbscan_params}")
print(f"Mejor Silhouette Score: {best_dbscan_score:.4f}")OPTIMIZACIÓN DE HIPERPARÁMETROS - DBSCAN
==================================================
Parámetros: {'eps': 0.3, 'min_samples': 3} | Silhouette: 0.6231 | Clusters: 3 | Ruido: 6
Parámetros: {'eps': 0.3, 'min_samples': 5} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 17
Parámetros: {'eps': 0.3, 'min_samples': 7} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 17
Parámetros: {'eps': 0.5, 'min_samples': 3} | Silhouette: 0.5574 | Clusters: 3 | Ruido: 0
Parámetros: {'eps': 0.5, 'min_samples': 5} | Silhouette: 0.5574 | Clusters: 3 | Ruido: 0
Parámetros: {'eps': 0.5, 'min_samples': 7} | Silhouette: 0.5574 | Clusters: 3 | Ruido: 0
Parámetros: {'eps': 0.7, 'min_samples': 3} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 0
Parámetros: {'eps': 0.7, 'min_samples': 5} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 0
Parámetros: {'eps': 0.7, 'min_samples': 7} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 0
Parámetros: {'eps': 0.9, 'min_samples': 3} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 0
Parámetros: {'eps': 0.9, 'min_samples': 5} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 0
Parámetros: {'eps': 0.9, 'min_samples': 7} | Silhouette: 0.6867 | Clusters: 2 | Ruido: 0
Mejores parámetros DBSCAN: {'eps': 0.3, 'min_samples': 5}
Mejor Silhouette Score: 0.68677.3 Optimización de MeanShift
# Optimización de hiperparámetros para MeanShift
print("\nOPTIMIZACIÓN DE HIPERPARÁMETROS - MEANSHIFT")
print("=" * 50)
# Estimar bandwidth base
base_bandwidth = estimate_bandwidth(pca_features)
print(f"Bandwidth base estimado: {base_bandwidth:.4f}")
# Parámetros a probar (múltiplos del bandwidth base)
bandwidth_multipliers = [0.5, 0.8, 1.0, 1.2, 1.5]
meanshift_params = [{'bandwidth': base_bandwidth * mult} for mult in bandwidth_multipliers]
best_meanshift_score = -1
best_meanshift_params = None
meanshift_results_opt = []
for params in meanshift_params:
model = MeanShift(**params)
model.fit(pca_features)
n_clusters = len(set(model.labels_))
silhouette = metrics.silhouette_score(pca_features, model.labels_)
result = {'params': params, 'silhouette_score': silhouette, 'n_clusters': n_clusters}
meanshift_results_opt.append(result)
print(f"Bandwidth: {params['bandwidth']:.4f} | Silhouette: {silhouette:.4f} | Clusters: {n_clusters}")
if silhouette > best_meanshift_score:
best_meanshift_score = silhouette
best_meanshift_params = params
print(f"\nMejores parámetros MeanShift: {best_meanshift_params}")
print(f"Mejor Silhouette Score: {best_meanshift_score:.4f}")OPTIMIZACIÓN DE HIPERPARÁMETROS - MEANSHIFT
==================================================
Bandwidth base estimado: 1.0495
Bandwidth: 0.5248 | Silhouette: 0.2639 | Clusters: 16
Bandwidth: 0.8396 | Silhouette: 0.6858 | Clusters: 2
Bandwidth: 1.0495 | Silhouette: 0.6858 | Clusters: 2
Bandwidth: 1.2594 | Silhouette: 0.5528 | Clusters: 3
Bandwidth: 1.5743 | Silhouette: 0.5528 | Clusters: 3
Mejores parámetros MeanShift: {'bandwidth': 0.8396011904761905}
Mejor Silhouette Score: 0.68588. Resultados Finales y Comparación
Finalmente, entrenamos los modelos con los mejores parámetros encontrados y comparamos los resultados:
# Comparación final con parámetros optimizados
print("\nCOMPARACIÓN FINAL CON PARÁMETROS OPTIMIZADOS")
print("=" * 60)
# Entrenar modelos con mejores parámetros
optimized_results = {}
optimized_models = {}
# KMeans optimizado
if best_kmeans_params:
kmeans_opt = KMeans(random_state=42, max_iter=1000, **best_kmeans_params).fit(pca_features)
kmeans_metrics_opt = evaluate_clustering(iris_labels, kmeans_opt.labels_, pca_features)
optimized_results['KMeans_Optimized'] = kmeans_metrics_opt
optimized_models['KMeans_Optimized'] = kmeans_opt
print(f"KMeans con parámetros: {best_kmeans_params}")
# DBSCAN optimizado (si se encontraron parámetros válidos)
if best_dbscan_params:
dbscan_opt = DBSCAN(**best_dbscan_params).fit(pca_features)
dbscan_metrics_opt = evaluate_clustering(iris_labels, dbscan_opt.labels_, pca_features)
optimized_results['DBSCAN_Optimized'] = dbscan_metrics_opt
optimized_models['DBSCAN_Optimized'] = dbscan_opt
print(f"DBSCAN con parámetros: {best_dbscan_params}")
else:
print("DBSCAN: No se pudieron optimizar parámetros")
# MeanShift optimizado
if best_meanshift_params:
meanshift_opt = MeanShift(**best_meanshift_params).fit(pca_features)
meanshift_metrics_opt = evaluate_clustering(iris_labels, meanshift_opt.labels_, pca_features)
optimized_results['MeanShift_Optimized'] = meanshift_metrics_opt
optimized_models['MeanShift_Optimized'] = meanshift_opt
print(f"MeanShift con parámetros: {best_meanshift_params}")COMPARACIÓN FINAL CON PARÁMETROS OPTIMIZADOS
============================================================
KMeans con parámetros: {'n_clusters': 2}
DBSCAN con parámetros: {'eps': 0.3, 'min_samples': 5}
MeanShift con parámetros: {'bandwidth': 0.8396011904761905}# Mostrar resultados
if optimized_results:
optimized_df = pd.DataFrame(optimized_results).T
optimized_df = optimized_df.round(4)
print("\nRESULTADOS CON PARÁMETROS OPTIMIZADOS:")
print(optimized_df)
else:
print("No se pudieron generar resultados optimizados")RESULTADOS CON PARÁMETROS OPTIMIZADOS:
Silhouette Score Adjusted Rand Score Homogeneity Score
KMeans_Optimized 0.6810 0.5681 0.5794
DBSCAN_Optimized 0.6867 0.5681 0.5794
MeanShift_Optimized 0.6858 0.5681 0.5794# Visualización final de resultados optimizados
n_models = len(optimized_models)
fig, axes = plt.subplots(1, n_models, figsize=(5*n_models, 5))
# Si solo hay un modelo, axes no será una lista
if n_models == 1:
axes = [axes]
colors = ['viridis', 'plasma', 'inferno']
for i, (title, model) in enumerate(optimized_models.items()):
scatter = axes[i].scatter(pca_features['PC1'], pca_features['PC2'],
c=model.labels_, cmap=colors[i % len(colors)],
s=100, alpha=0.7, edgecolors='black')
axes[i].set_title(f'{title}\nSilhouette: {optimized_results[title]["Silhouette Score"]:.4f}')
axes[i].set_xlabel('PC1')
axes[i].set_ylabel('PC2')
axes[i].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("\n¡Análisis de clustering completado!")¡Análisis de clustering completado!
Visualización final de los clusters encontrados por cada algoritmo optimizado en el espacio PCA 2D
Material de Práctica
Para consolidar los conceptos aprendidos sobre clustering, te invito a practicar con este ejercicio completo:
- Workflow Completo de Clustering - Dataset Iris - Implementa y compara diferentes algoritmos de clustering con optimización de hiperparámetros.
Ejercicio adicional: Prueba aplicar este mismo workflow a otros datos como Penguin o Wine datasets. Observa cómo cambian los resultados según las características de los datos y experimenta con diferentes métricas de evaluación.
Referencias
Para profundizar en algoritmos de clustering con Python, recomendamos consultar estos recursos:
- Clustering - Scikit-learn Documentation, la documentación oficial de scikit-learn sobre algoritmos de clustering, con ejemplos detallados y comparaciones entre diferentes métodos.
- The 5 Clustering Algorithms Data Scientists Need to Know, un artículo completo de Towards Data Science que explica los algoritmos de clustering más importantes con ejemplos prácticos en Python.