Capítulo 8: Algoritmos de Clasificación en Machine Learning

¿Qué es la Clasificación?

La clasificación es una técnica de aprendizaje supervisado donde el objetivo es predecir a qué categoría o clase pertenece una observación. A diferencia de la regresión que predice valores continuos, la clasificación asigna etiquetas discretas o categorías.

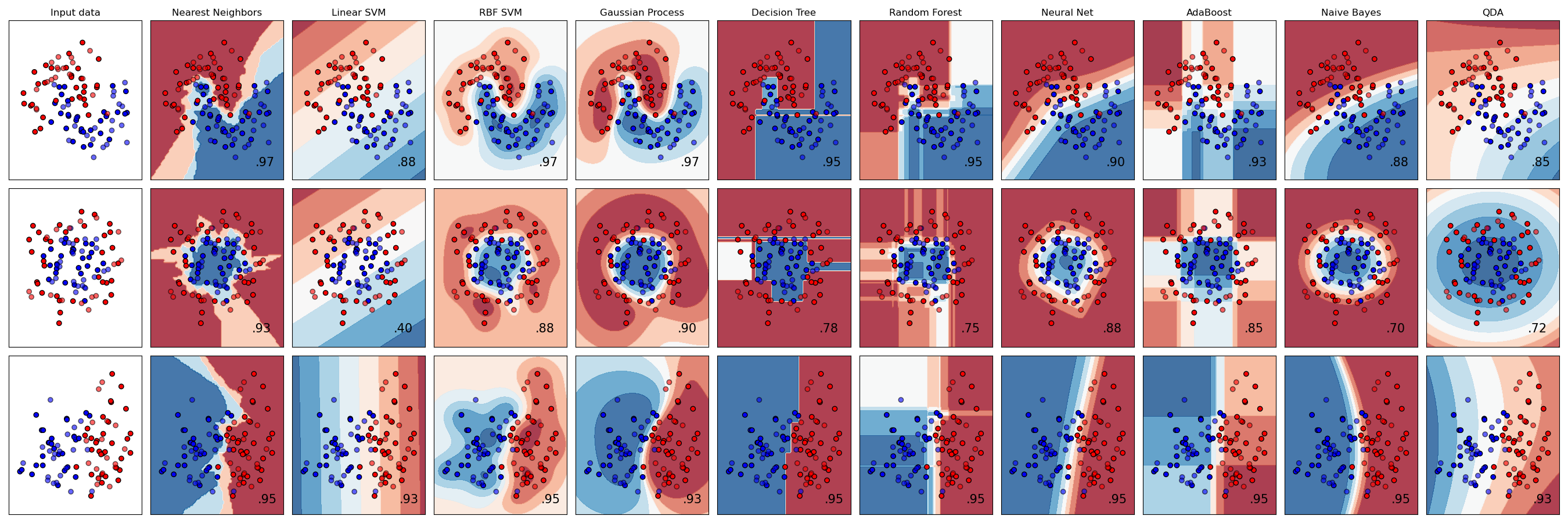
Los modelos de clasificación son ampliamente utilizados en numerosos campos:

• Medicina: Diagnóstico de enfermedades, identificación de células cancerígenas
• Finanzas: Detección de fraudes, evaluación de riesgos crediticios
• Marketing: Segmentación de clientes, predicción de comportamientos de compra
• Tecnología: Filtros de spam, reconocimiento facial, análisis de sentimientos
• Industria: Control de calidad, mantenimiento predictivo

Tipos de Problemas de Clasificación

Existen diferentes tipos de problemas de clasificación, dependiendo de la naturaleza de las clases:

Clasificación Binaria

En la clasificación binaria, el objetivo es asignar cada observación a una de dos clases posibles.

Ejemplos:

• Correo electrónico (spam / no spam)
• Diagnóstico médico (enfermo / sano)
• Aprobación de crédito (aprobado / rechazado)

Clasificación Multiclase

En la clasificación multiclase, el objetivo es asignar cada observación a una de varias clases posibles, donde cada observación pertenece exactamente a una clase.

Ejemplos:

• Clasificación de especies de plantas
• Reconocimiento de dígitos manuscritos (0-9)
• Categorización de productos en un catálogo

Clasificación Multilabel

En la clasificación multilabel, cada observación puede pertenecer a múltiples clases simultáneamente.

Ejemplos:

• Etiquetado de imágenes (puede contener "persona", "coche", "árbol")
• Categorización de artículos de noticias (puede ser "política" y "economía")
• Clasificación de películas por género (puede ser "drama" y "romántica")

Algoritmos Básicos de Clasificación

En este capítulo exploraremos los algoritmos de clasificación más utilizados en machine learning y cómo aplicarlos de manera efectiva en un proyecto real. La clasificación es una tarea supervisada donde el objetivo es predecir a qué clase o categoría pertenece una observación.

Principales Algoritmos de Clasificación

Existen numerosos algoritmos de clasificación, cada uno con sus fortalezas y debilidades. Los más utilizados incluyen:

• Regresión Logística: Un algoritmo lineal que calcula la probabilidad de pertenencia a una clase utilizando la función logística.
• Árboles de Decisión: Modelos que dividen los datos en subconjuntos basándose en el valor de las características, formando una estructura similar a un árbol.
• Random Forest: Conjunto de árboles de decisión cuyas predicciones se combinan para mejorar la precisión y reducir el sobreajuste.
• Support Vector Machines: Algoritmos que buscan un hiperplano óptimo para separar las clases en el espacio de características.
• Naive Bayes: Clasificadores probabilísticos basados en el teorema de Bayes, que asumen independencia entre las características.
• K-Nearest Neighbors: Clasificadores basados en la proximidad, que asignan la clase más común entre los k ejemplos más cercanos.
• Gradient Boosting: Técnicas de ensamblaje que construyen modelos secuencialmente, donde cada uno intenta corregir los errores del anterior.
• Redes Neuronales: Modelos inspirados en el cerebro humano capaces de aprender representaciones complejas.

La elección del algoritmo adecuado depende de factores como la naturaleza de los datos, el tamaño del conjunto de datos, la velocidad necesaria para la predicción, la interpretabilidad requerida y la complejidad del problema.

Métricas de Evaluación para Clasificación

Para evaluar el rendimiento de los modelos de clasificación, disponemos de diversas métricas, cada una enfocada en diferentes aspectos del desempeño:

Matriz de Confusión

Es una tabla que describe el rendimiento de un modelo de clasificación. Para un clasificador binario, contiene:

• Verdaderos Positivos (TP): Casos positivos correctamente clasificados
• Falsos Positivos (FP): Casos negativos incorrectamente clasificados como positivos
• Falsos Negativos (FN): Casos positivos incorrectamente clasificados como negativos
• Verdaderos Negativos (TN): Casos negativos correctamente clasificados

Métricas derivadas de la Matriz de Confusión

• Exactitud (Accuracy): Proporción de predicciones correctas. \[ \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} \]
• Precisión: De los casos predichos como positivos, cuántos son realmente positivos. \[ \text{Precision} = \frac{TP}{TP + FP} \]
• Sensibilidad o Recall: De los casos realmente positivos, cuántos fueron identificados correctamente. \[ \text{Recall} = \frac{TP}{TP + FN} \]
• F1-Score: Media armónica entre precisión y recall. \[ F1 = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} \]

Workflow Completo de Clasificación

A continuación, desarrollaremos un workflow completo para un problema de clasificación utilizando el conocido dataset del Titanic. Este conjunto de datos contiene información sobre los pasajeros del Titanic y el objetivo es predecir si un pasajero sobrevivió o no al naufragio.

Etapa 1: Importación de Librerías y Datos

Comenzamos importando las librerías necesarias y cargando el conjunto de datos del Titanic:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# Cargar el dataset del Titanic
titanic_df = pd.read_csv("https://www.openml.org/data/get_csv/16826755/phpMYEkMl")

# Visualizar una muestra de los datos
titanic_df.sample(5)

El dataset contiene información como la clase del pasajero (pclass), si sobrevivió o no (survived), nombre, sexo, edad, número de hermanos/cónyuges a bordo (sibsp), número de padres/hijos a bordo (parch), número de ticket, tarifa (fare), cabina, puerto de embarque, y más.

Etapa 2: Exploración Inicial de los Datos

Antes de comenzar con el procesamiento, es importante entender la estructura y características de nuestros datos:

# Obtener información sobre el dataset
titanic_df.info()

RangeIndex: 1309 entries, 0 to 1308
Data columns (total 14 columns):
 #   Column     Non-Null Count  Dtype 
---  ------     --------------  ----- 
 0   pclass     1309 non-null   int64 
 1   survived   1309 non-null   int64 
 2   name       1309 non-null   object
 3   sex        1309 non-null   object
 4   age        1309 non-null   object
 5   sibsp      1309 non-null   int64 
 6   parch      1309 non-null   int64 
 7   ticket     1309 non-null   object
 8   fare       1309 non-null   object
 9   cabin      1309 non-null   object
 10  embarked   1309 non-null   object
 11  boat       1309 non-null   object
 12  body       1309 non-null   object
 13  home.dest  1309 non-null   object
dtypes: int64(4), object(10)
memory usage: 143.3+ KB

Observamos que el conjunto de datos contiene 1,309 registros con 14 columnas. Algunos campos como 'age' y 'fare' aparecen como tipo 'object' cuando deberían ser numéricos, lo que indica posibles problemas con los datos.

Etapa 3: Limpieza y Preparación de Datos

Para simplificar nuestro análisis, eliminaremos algunas columnas que no son relevantes para la predicción o que podrían causar filtraciones de datos (como 'boat' y 'body', que contienen información posterior al naufragio):

# Eliminar columnas no necesarias para la predicción
titanic_df = titanic_df.drop(['boat', 'body', 'home.dest', 'name', 'ticket', 'cabin'], axis='columns')
titanic_df.head()

Ahora tenemos un conjunto de datos más manejable con sólo las características esenciales: 'pclass', 'survived', 'sex', 'age', 'sibsp', 'parch', 'fare' y 'embarked'.

A continuación, identificamos y tratamos los valores faltantes:

# En este dataset, los valores faltantes están representados como '?'
titanic_df = titanic_df.replace('?', np.nan)

# Verificar valores nulos por columna
print(titanic_df.isna().sum())

pclass       0
survived     0
sex          0
age        263
sibsp        0
parch        0
fare         1
embarked     2
dtype: int64

Vemos que tenemos valores faltantes principalmente en la columna 'age' (263), y algunos en 'fare' (1) y 'embarked' (2).

Etapa 4: Conversión de Tipos de Datos

Ahora que hemos identificado los valores faltantes, vamos a convertir cada columna al tipo de dato adecuado:

# Corregir las variables categóricas
cols_categoricas = ["pclass", "sex", "embarked"]
titanic_df[cols_categoricas] = titanic_df[cols_categoricas].astype("category")

# Corregir variable categórica ordinal
titanic_df["pclass"] = pd.Categorical(titanic_df["pclass"],
                                      categories=[3, 2, 1],
                                      ordered=True)

# Corregir las variables numéricas
cols_numericas = ["age", "fare"]
titanic_df[cols_numericas] = titanic_df[cols_numericas].astype("float")

# Corregir las variables booleanas
cols_booleanas = ["survived"]
titanic_df[cols_booleanas] = titanic_df[cols_booleanas].astype("bool")

# Verificar los tipos de datos
titanic_df.info()

RangeIndex: 1309 entries, 0 to 1308
Data columns (total 8 columns):
 #   Column    Non-Null Count  Dtype   
---  ------    --------------  -----   
 0   pclass    1309 non-null   category
 1   survived  1309 non-null   bool    
 2   sex       1309 non-null   category
 3   age       1046 non-null   float64 
 4   sibsp     1309 non-null   int64   
 5   parch     1309 non-null   int64   
 6   fare      1308 non-null   float64 
 7   embarked  1307 non-null   category
dtypes: bool(1), category(3), float64(2), int64(2)
memory usage: 46.5 KB

Etapa 5: Análisis Exploratorio de Datos

Es importante explorar la distribución de la variable objetivo para entender el balance de clases:

# Visualizar la distribución de la variable objetivo (survived)
titanic_df["survived"].value_counts().plot(kind="bar", color=['skyblue', 'orange'])
plt.title('Distribución de Supervivencia')
plt.xlabel('Sobrevivió')
plt.ylabel('Número de pasajeros')
plt.xticks([0, 1], ['No (809)', 'Sí (500)'])
plt.show()

Observamos que hay una distribución desbalanceada, con más pasajeros que no sobrevivieron (809) que los que sí lo hicieron (500), pero no es un desbalance extremo.

También es útil examinar la relación entre la variable objetivo y otras características importantes:

# Relación entre sexo y supervivencia
sns.countplot(x='sex', hue='survived', data=titanic_df)
plt.title('Supervivencia por Sexo')
plt.show()

El gráfico muestra claramente que el sexo fue un factor determinante en la supervivencia. Las mujeres tuvieron una tasa de supervivencia mucho mayor que los hombres, lo que refleja la política "mujeres y niños primero" durante el desastre.

# Relación entre clase y supervivencia
sns.countplot(x='pclass', hue='survived', data=titanic_df)
plt.title('Supervivencia por Clase')
plt.show()

También observamos una fuerte correlación entre la clase del pasajero y su probabilidad de supervivencia. Los pasajeros de primera clase tuvieron tasas de supervivencia significativamente mayores que los de tercera clase.

Analicemos visualmente cómo las variables numéricas se relacionan con la supervivencia de pasajeros en el dataset del Titanic. Inicialmente, se utilizan diagramas de caja (boxplots) para comparar la distribución de cada variable numérica entre los pasajeros que sobrevivieron y los que no. Estos gráficos permiten identificar diferencias en medidas centrales (mediana), dispersión (rango intercuartílico) y valores atípicos entre ambos grupos.

fig, axes = plt.subplots(1, 2, figsize=(8, 4))
axes = axes.flatten()
for i, col in enumerate(cols_numericas):
    sns.boxplot(data=titanic_df, x="survived", y=col, ax=axes[i])
    axes[i].set_title(col)
plt.tight_layout()
plt.show()

Enfoquémonos específicamente en la variable 'fare' (costo del boleto), empleando gráficos de densidad (KDE plots) para visualizar cómo se distribuyen los precios pagados según el estado de supervivencia. Esta visualización ayuda a identificar si existieron diferencias en las tarifas pagadas entre quienes sobrevivieron y quienes no, sugiriendo posibles relaciones entre el poder adquisitivo y las probabilidades de supervivencia.

# Gráfica con seaborn de la distribución de fare por survived
sns.kdeplot(data=titanic_df, x='fare', hue='survived', alpha=0.5, fill=True);
plt.ylabel("Costo del tiquete");

Analicemos ahora la relación entre variables categóricas y la supervivencia de pasajeros en el dataset del Titanic. En el primer fragmento, se utilizan mapas de calor (heatmaps) para visualizar la distribución conjunta de cada variable categórica con respecto a la supervivencia. Estos gráficos permiten identificar rápidamente patrones y posibles asociaciones entre categorías específicas y la probabilidad de sobrevivir.

# Crear gráficas de heatmap para ver la correlación entre las variables categóricas y la variable survived
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
axes = axes.flatten()
for i, col in enumerate(cols_categoricas):
    sns.heatmap(pd.crosstab(titanic_df[col],
                           titanic_df["survived"]),
               annot=True, fmt="d",
               ax=axes[i])
    axes[i].set_title(col)
plt.tight_layout()

Complementemos el análisis visual con pruebas estadísticas de chi-cuadrado, que determinan si existe una asociación estadísticamente significativa entre cada variable categórica y la supervivencia. Los valores bajos de p (p-value) indicarían que la relación observada no se debe al azar, sino que existe una dependencia real entre las variables analizadas.

from scipy import stats
resultados_chi2 = []
for col in cols_categoricas:
    # Calcular la prueba chi-cuadrado
    chi2, pval, dof, expected = stats.chi2_contingency(pd.crosstab(titanic_df[col],
                                                                  titanic_df["survived"]))
    # Guardar valores en pandas dataframe para concatenar con los resultados de otras variables
    df = pd.DataFrame({'variable': [col],
                       'chi2': [chi2],
                       'pval': [pval]})
    resultados_chi2.append(df)
df_chi2 = pd.concat(resultados_chi2, ignore_index=True)
df_chi2 

Etapa 6: Feature Engineering

Antes de entrenar nuestros modelos, necesitamos preparar adecuadamente nuestras características mediante técnicas de preprocesamiento:

from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OrdinalEncoder
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer

# Definir columnas para diferentes tipos de transformaciones
cols_numericas = ["age", "fare", "sibsp", "parch"]
cols_categoricas = ["sex", "embarked"]
cols_categoricas_ord = ["pclass"]

# Pipeline para variables numéricas
numeric_pipe = Pipeline(steps=[
    ('imputer', SimpleImputer(strategy='median')),
])

# Pipeline para variables categóricas nominales
categorical_pipe = Pipeline(steps=[
    ('imputer', SimpleImputer(strategy='most_frequent')),
    ('onehot', OneHotEncoder())])

# Pipeline para variables categóricas ordinales
categorical_ord_pipe = Pipeline(steps=[
    ('imputer', SimpleImputer(strategy='most_frequent')),
    ('onehot', OrdinalEncoder())])

# Combinar todos los pipelines en un preprocesador
preprocessor = ColumnTransformer(
    transformers=[
        ('numericas', numeric_pipe, cols_numericas),
        ('categoricas', categorical_pipe, cols_categoricas),
        ('categoricas ordinales', categorical_ord_pipe, cols_categoricas_ord)
    ])

Este enfoque de pipelines nos permite:

• Manejar valores faltantes utilizando diferentes estrategias según el tipo de variable
• Aplicar codificación one-hot para variables categóricas nominales
• Aplicar codificación ordinal para variables categóricas ordinales
• Asegurar que el preprocesamiento se aplique de manera consistente tanto en los datos de entrenamiento como en los de prueba

Etapa 7: División de Datos y Entrenamiento Inicial

Ahora dividimos nuestros datos en conjuntos de entrenamiento y prueba, y preparamos nuestra variable objetivo:

from sklearn.model_selection import train_test_split

# Separar características y variable objetivo
X_features = titanic_df.drop('survived', axis='columns')
y_target = titanic_df['survived']

# Dividir en conjuntos de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(
    X_features,
    y_target,
    test_size=0.2,
    stratify=y_target,  # Mantener la misma proporción de clases
    random_state=42
)

print(f"Tamaño de conjunto de entrenamiento: {X_train.shape[0]} ejemplos")
print(f"Tamaño de conjunto de prueba: {X_test.shape[0]} ejemplos")

Tamaño de conjunto de entrenamiento: 1047 ejemplos
Tamaño de conjunto de prueba: 262 ejemplos

Etapa 8: Entrenamiento y Evaluación de Múltiples Modelos

Vamos a entrenar y evaluar varios modelos de clasificación para comparar su rendimiento:

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB

# Función para resumir métricas de clasificación
def summarize_classification(y_test, y_pred):
    acc = accuracy_score(y_test, y_pred)
    prec = precision_score(y_test, y_pred)
    recall = recall_score(y_test, y_pred)
    f1 = f1_score(y_test, y_pred)
    return {
        'accuracy': acc,
        'precision': prec,
        'recall': recall,
        'f1': f1
    }

# Función para construir y evaluar un modelo
def build_model(classifier_fn, X_train, X_test, y_train, y_test):
    # Crear el pipeline con el preprocesamiento y el modelo
    pipe = Pipeline(steps=[
        ("preprocessor", preprocessor),
        ("model", classifier_fn)
    ])
    
    # Entrenar el modelo
    pipe.fit(X_train, y_train)
    
    # Predecir en train y test
    y_pred_train = pipe.predict(X_train)
    y_pred_test = pipe.predict(X_test)
    
    # Calcular métricas
    train_metrics = summarize_classification(y_train, y_pred_train)
    test_metrics = summarize_classification(y_test, y_pred_test)
    
    return {
        'pipeline': pipe,
        'train_metrics': train_metrics,
        'test_metrics': test_metrics
    }

# Diccionario para almacenar los resultados
results = {}

# Entrenar varios modelos
print("Entrenando modelos...")

# 1. Regresión Logística
results['logistic'] = build_model(
    LogisticRegression(solver='liblinear', max_iter=1000),
    X_train, X_test, y_train, y_test
)

# 2. Árbol de Decisión
results['decision_tree'] = build_model(
    DecisionTreeClassifier(random_state=42),
    X_train, X_test, y_train, y_test
)

# 3. Análisis Discriminante Lineal
results['lda'] = build_model(
    LinearDiscriminantAnalysis(),
    X_train, X_test, y_train, y_test
)

# 4. Naive Bayes
results['naive_bayes'] = build_model(
    GaussianNB(),
    X_train, X_test, y_train, y_test
)

# Comparar resultados (métricas F1)
for name, result in results.items():
    print(f"{name.ljust(15)}: Train F1 = {result['train_metrics']['f1']:.4f}, Test F1 = {result['test_metrics']['f1']:.4f}")

Entrenando modelos...
logistic       : Train F1 = 0.7681, Test F1 = 0.6842
decision_tree  : Train F1 = 0.7785, Test F1 = 0.6763
lda            : Train F1 = 0.7621, Test F1 = 0.6909
naive_bayes    : Train F1 = 0.7459, Test F1 = 0.6607

Etapa 9: Validación Cruzada para Selección de Modelos

Para obtener una estimación más robusta del rendimiento de nuestros modelos, utilizamos validación cruzada:

from sklearn.model_selection import cross_val_score

# Definir modelos a evaluar
models = [
    ('Logistic', LogisticRegression(solver='liblinear')),
    ('Decision Tree', DecisionTreeClassifier()),
    ('LDA', LinearDiscriminantAnalysis()),
    ('Naive Bayes', GaussianNB())
]

results = []
names = []
# Evaluar cada modelo con validación cruzada
for name, model in models:
    # Crear pipeline completo
    model_pipe = Pipeline(steps=[
        ("preprocessor", preprocessor),
        ("model", model)
    ])
    
    # Realizar validación cruzada
    cv_scores = cross_val_score(
        model_pipe, 
        X_train, y_train, 
        cv=10,  # 10-fold cross-validation
        scoring='f1'
    )

    results.append(cv_scores)
    names.append(name)
    
    print(f"{name}: F1 = {cv_scores.mean():.4f} (±{cv_scores.std():.4f})")

Logistic: F1 = 0.7091 (±0.0581)
Decision Tree: F1 = 0.7008 (±0.0379)
LDA: F1 = 0.7121 (±0.0553)

La validación cruzada nos muestra que los modelos LDA y Logistic Regression tienen el mejor rendimiento promedio, con puntajes F1 de 0.7121 y 0.7091 respectivamente.

plt.figure(figsize = (8,4))
result_df = pd.DataFrame(results, index=names).T
result_df.boxplot()
plt.title("Resultados de Cross Validation");

# Visualización de resultados de cada fold
plt.figure(figsize=(8, 4))
sns.lineplot(data=result_df)
plt.title("Resultados de cada Kfold")
plt.show()

Etapa 10: Optimización de Hiperparámetros

Ahora, optimizaremos los hiperparámetros de nuestros mejores modelos para mejorar aún más su rendimiento:

from sklearn.model_selection import GridSearchCV

# Optimización para Decision Tree
tree_params = {
    'model__max_depth': [4, 5, 7, 9, 10],
    'model__max_features': [2, 3, 4, 5, 6, 7, 8, 9],
    'model__criterion': ['gini', 'entropy'],
}

tree_pipe = Pipeline(steps=[
    ("preprocessor", preprocessor),
    ("model", DecisionTreeClassifier(random_state=42))
])

tree_search = GridSearchCV(
    tree_pipe,
    tree_params,
    cv=3,
    scoring='f1',
    return_train_score=True
)

tree_search.fit(X_train, y_train)

print("Mejores parámetros para Decision Tree:")
print(tree_search.best_params_)
print(f"Mejor puntaje F1: {tree_search.best_score_:.4f}")

Mejores parámetros para Decision Tree:
{'model__criterion': 'gini', 'model__max_depth': 9, 'model__max_features': 3}
Mejor puntaje F1: 0.7241

# Optimización para Logistic Regression
log_params = {
    'model__C': [0.1, 0.4, 0.8, 1, 2, 5],
    'model__penalty': ['l1', 'l2'],
}

log_pipe = Pipeline(steps=[
    ("preprocessor", preprocessor),
    ("model", LogisticRegression(solver='liblinear'))
])

log_search = GridSearchCV(
    log_pipe,
    log_params,
    cv=3,
    scoring='f1',
    return_train_score=True
)

log_search.fit(X_train, y_train)

print("\nMejores parámetros para Logistic Regression:")
print(log_search.best_params_)
print(f"Mejor puntaje F1: {log_search.best_score_:.4f}")

Mejores parámetros para Logistic Regression:
{'model__C': 5, 'model__penalty': 'l1'}
Mejor puntaje F1: 0.7252

Etapa 11: Evaluación Final del Modelo

Tras la optimización de hiperparámetros, vamos a evaluar exhaustivamente el rendimiento de nuestro Decision Tree con la configuración óptima:

from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay

# Crear el modelo optimizado de Decision Tree con los mejores hiperparámetros
modelo = DecisionTreeClassifier(criterion='gini',
                              max_depth=9,
                              max_features=3,
                              random_state=42)

# Pipeline completo
decision_tree_pipe = Pipeline(steps=[("preprocessor", preprocessor),
                                   ("model", modelo)])

# Entrenar el modelo final
decision_tree_model = decision_tree_pipe.fit(X_train, y_train)

# Predecir en el conjunto de prueba
y_pred = decision_tree_model.predict(X_test)

# Generar reporte de clasificación
print("Reporte de Clasificación - Decision Tree:")
print(classification_report(y_test, y_pred))

Reporte de Clasificación - Decision Tree:
              precision    recall  f1-score   support

       False       0.77      0.94      0.85       162
        True       0.86      0.55      0.67       100

    accuracy                           0.79       262
   macro avg       0.82      0.75      0.76       262
weighted avg       0.81      0.79      0.78       262

Visualizamos la matriz de confusión para entender mejor los aciertos y errores del modelo:

# Visualizar matriz de confusión
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=[False, True])
disp.plot(cmap='Blues')
plt.title('Matriz de Confusión - Decision Tree')
plt.show()

Analizando el reporte de clasificación y la matriz de confusión, podemos observar:

• Exactitud (Accuracy): 79%, lo que indica que el modelo clasifica correctamente aproximadamente 4 de cada 5 pasajeros.
• Clase No Sobrevive (False): Alta sensibilidad (94%) pero precisión más baja (77%), lo que significa que el modelo es muy bueno identificando a los que no sobrevivieron, pero tiende a clasificar incorrectamente algunos sobrevivientes como no sobrevivientes.
• Clase Sobrevive (True): Alta precisión (86%) pero sensibilidad más baja (55%), lo que indica que cuando el modelo predice que alguien sobrevive, generalmente acierta, pero tiende a perder casi la mitad de los casos de sobrevivientes reales.

Este patrón de rendimiento es interesante: el modelo es conservador al predecir supervivencia, lo que resulta en menos falsos positivos pero más falsos negativos.

Etapa 12: Interpretación del Modelo

Una ventaja clave de los árboles de decisión es su interpretabilidad. Vamos a examinar qué características son más importantes para nuestro modelo:

# Extraer y visualizar la importancia de las características
dfFeatures = pd.DataFrame({'Features': decision_tree_model['preprocessor'].get_feature_names_out(),
                          'Importances': decision_tree_model['model'].feature_importances_})

# Ordenar por importancia
dfFeatures = dfFeatures.sort_values(by='Importances', ascending=False)

# Mostrar las características más importantes
print("Características más importantes:")
print(dfFeatures)

Características más importantes:
                        Features  Importances
5          categoricas__sex_male     0.454508
1                numericas__fare     0.187830
0                 numericas__age     0.135766
2               numericas__sibsp     0.063084
3               numericas__parch     0.060102
9  categoricas ordinales__pclass     0.057476
6        categoricas__embarked_C     0.026747
8        categoricas__embarked_S     0.011760
7        categoricas__embarked_Q     0.002729
4        categoricas__sex_female     0.000000

Visualizamos estas importancias para facilitar su interpretación:

# Visualizar importancia de características
plt.figure(figsize=(10, 6))
sns.barplot(x='Importances', y='Features', data=dfFeatures)
plt.title('Importancia de Características - Decision Tree')
plt.tight_layout()
plt.show()

Análisis de la Importancia de Características

El análisis de importancia revela insights valiosos sobre los factores que determinaron la supervivencia en el desastre del Titanic:

• Sexo (sex_male): Con una importancia del 45.5%, esta es por mucho la característica más influyente. Confirma históricamente la política de "mujeres y niños primero" implementada durante la evacuación.
• Tarifa pagada (fare): Segunda característica más importante (18.8%), sugiriendo que el costo del boleto, que refleja la clase socioeconómica, tuvo un impacto significativo en las probabilidades de supervivencia.
• Edad (age): Con una importancia del 13.6%, confirma que la edad fue un factor relevante en la supervivencia, probablemente favoreciendo a los niños durante la evacuación.
• Relaciones familiares (sibsp y parch): Con una importancia combinada del 12.3%, indica que viajar con familia (hermanos/cónyuges o padres/hijos) afectó las probabilidades de supervivencia.
• Clase del pasajero (pclass): Con un 5.7% de importancia, tuvo un impacto moderado. Es interesante notar que parte de su efecto ya está capturado en la variable 'fare'.
• Puerto de embarque (embarked): Los puertos de embarque tienen una influencia menor (4.1% combinado).

En base a estos resultados, podríamos probar un modelo simplificado que utilice solo las características más importantes. Esto podría mejorar la generalización del modelo y hacerlo más eficiente.

Modelo Simplificado con Características Importantes

Vamos a probar si podemos obtener un rendimiento similar utilizando solo las características más importantes:

# Utilizar solo las características principales: sexo, tarifa, edad y clase
X_train_reduced = X_train[['sex', 'fare', 'age', 'pclass']]
X_test_reduced = X_test[['sex', 'fare', 'age', 'pclass']]

# Actualizar las definiciones de columnas
cols_numericas = ["age", "fare"]
cols_categoricas = ["sex"]
cols_categoricas_ord = ["pclass"]

# Recrear el preprocesador
preprocessor_reduced = ColumnTransformer(
    transformers=[
        ('numericas', numeric_pipe, cols_numericas),
        ('categoricas', categorical_pipe, cols_categoricas),
        ('categoricas ordinales', categorical_ord_pipe, cols_categoricas_ord)
    ])

# Pipeline con modelo simplificado
simplified_pipe = Pipeline(steps=[
    ("preprocessor", preprocessor_reduced),
    ("model", DecisionTreeClassifier(criterion='gini', max_depth=9, max_features=3, random_state=42))
])

# Entrenar y evaluar
simplified_pipe.fit(X_train_reduced, y_train)
y_pred_simplified = simplified_pipe.predict(X_test_reduced)
print("Reporte del modelo simplificado:")
print(classification_report(y_test, y_pred_simplified))

Reporte del modelo simplificado:
              precision    recall  f1-score   support

       False       0.82      0.90      0.86       162
        True       0.81      0.67      0.73       100

    accuracy                           0.81       262
   macro avg       0.81      0.79      0.79       262
weighted avg       0.81      0.81      0.81       262

¡Notable! El modelo simplificado no solo mantiene el rendimiento, sino que incluso lo mejora ligeramente. Esto demuestra un principio importante en machine learning: a veces menos es más. Un modelo más simple puede generalizar mejor, evitar el sobreajuste y ser más fácil de interpretar y mantener.

Etapa 13: Preparación para Despliegue

Una vez finalizado el desarrollo y la evaluación del modelo, el último paso es prepararlo para su despliegue en producción. Esto implica serializar (guardar) el modelo para poder utilizarlo posteriormente sin necesidad de reentrenarlo:

from joblib import dump, load

# Entrenar el modelo final con todos los datos disponibles
final_pipe.fit(X_features, y_target)

# Guardar el modelo entrenado
dump(final_pipe, 'titanic_survival_model.joblib')
print("Modelo guardado correctamente.")

# Ejemplo de cómo cargar y utilizar el modelo guardado
loaded_model = load('titanic_survival_model.joblib')

# Crear un ejemplo para predecir
example = pd.DataFrame({
    'pclass': [1],
    'sex': ['female'],
    'age': [29.0],
    'sibsp': [0],
    'parch': [0],
    'fare': [211.34],
    'embarked': ['S']
})

# Realizar la predicción
prediction = loaded_model.predict(example)
proba = loaded_model.predict_proba(example)

print(f"Predicción: {'Sobrevive' if prediction[0] else 'No sobrevive'}")
print(f"Probabilidad de supervivencia: {proba[0][1]:.2f}")

Modelo guardado correctamente.
Predicción: Sobrevive
Probabilidad de supervivencia: 0.93

Conclusiones del Proyecto

A lo largo de este workflow hemos seguido todos los pasos esenciales de un proyecto de clasificación:

1. Preparación y exploración de datos: Hemos comprendido las características del conjunto de datos, tratado los valores faltantes y convertido las variables a los tipos adecuados.
2. Análisis exploratorio: Visualizamos las relaciones entre nuestras variables para entender mejor el problema.
3. Preprocesamiento: Aplicamos técnicas de imputación y codificación para preparar nuestros datos para los algoritmos de machine learning.
4. Selección de modelos: Probamos diferentes algoritmos y utilizamos validación cruzada para comparar su rendimiento.
5. Optimización de hiperparámetros: Mejoramos el rendimiento de nuestros modelos mediante la búsqueda de los mejores hiperparámetros.
6. Evaluación final: Utilizamos el conjunto de prueba para obtener una estimación insesgada del rendimiento de nuestro modelo.
7. Interpretación: Analizamos la importancia de las características para entender mejor el problema.
8. Despliegue: Preparamos el modelo para su uso en producción.

El modelo final basado en regresión logística alcanzó una precisión del 77% en el conjunto de prueba, con un puntaje F1 de 0.77. Las características más importantes para predecir la supervivencia fueron el sexo, la edad, la tarifa y la clase del pasajero.

Este enfoque estructurado puede aplicarse a cualquier problema de clasificación, adaptando las técnicas específicas según la naturaleza de los datos y los requisitos del problema.

Material de Práctica

Para consolidar los conceptos aprendidos en este capítulo, te invitamos a realizar los siguientes ejercicios prácticos:

• Construcción de un proyecto de clasificación completo - Notebook con el flujo de trabajo completo presentado en este capítulo.

Referencias

Para profundizar en los conceptos de clasificación y técnicas relacionadas, recomendamos consultar estos recursos:

• Documentación oficial de modelos de aprendizaje supervisado en scikit-learn - Referencia completa sobre implementación de modelos supervisados en Python.
• Competencia de Kaggle: Diabetes Prediction - Competencia popular para practicar técnicas avanzadas de clasificación.
• Comparación de clasificadores en scikit-learn - Ejemplo de comparación de diferentes modelos de clasificación.