KNN vs. Regresión Lineal: Dos perspectivas en Aprendizaje Automático
Published:
Si estás adentrándote en el mundo del aprendizaje automático, probablemente te hayas encontrado con términos como Regresión Lineal y K-Nearest Neighbors (KNN). Estos son algoritmos fundamentales que sirven como bloques de construcción para modelos más complejos. Comprender cómo funcionan y cuándo usarlos es crucial para cualquiera que desee profundizar en ciencia de datos.
En este artículo, exploraremos la Regresión Lineal y la Regresión K-Nearest Neighbors de una manera amigable para principiantes. Desglosaremos términos complejos en un lenguaje sencillo, proporcionaremos explicaciones intuitivas y revisaremos ejemplos de código en Python para consolidar tu comprensión.
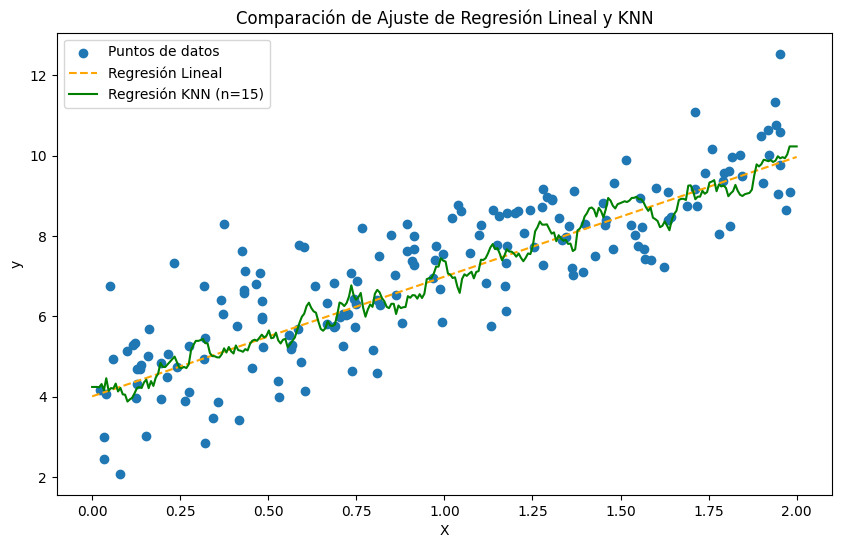
Ajuste de Regresión Lineal vs. Ajuste de Regresión KNN
¿Qué es la Regresión Lineal?
En esencia, la Regresión Lineal es un método para modelar la relación entre una variable dependiente (lo que intentas predecir) y una o más variables independientes (las características que usas para predecir). Asume que esta relación es lineal — es decir, puede representarse con una línea recta. Por ejemplo, estás tratando de predecir la estatura de alguien en función de su edad. Si trazas la edad en el eje x y la estatura en el eje y, la Regresión Lineal intenta encontrar la línea recta que mejor se ajusta a tus puntos de datos.
Ecuación del modelo de Regresión Lineal: ŷ = β₀ + β₁x + ε
- ŷ es la variable dependiente.
- x es la variable independiente.
- β₀ es el intercepto (el valor de ŷ cuando x = 0).
- β₁ es la pendiente de la línea (cuánto cambia ŷ por una unidad de cambio en x).
- ε es el término de error (la diferencia entre los valores predichos y los reales).
Ventajas de la Regresión Lineal
Simplicidad: La regresión lineal es fácil de entender y aplicar. Se basa en una fórmula matemática simple para describir la relación entre variables, lo que la hace accesible incluso para quienes son nuevos en estadística. Al trazar una línea recta a través de los datos, muestra cómo una variable (la dependiente) cambia con respecto a otra (la independiente) o, en el caso de la regresión lineal múltiple, con respecto a varias variables.
Eficiencia: Dado que la regresión lineal solo requiere estimar unos pocos parámetros (como el intercepto y las pendientes para cada variable), es computacionalmente ligera y se ejecuta de manera eficiente, incluso en conjuntos de datos grandes. Esta simplicidad permite implementarla rápidamente y con recursos mínimos, lo que la hace ideal para análisis exploratorios o modelado inicial.
Interpretabilidad: Una de las mayores ventajas de la regresión lineal es que proporciona resultados fácilmente interpretables. Cada coeficiente (como β₀ para el intercepto y β₁ para la pendiente) tiene un significado claro. El intercepto β₀ representa el valor de la variable dependiente cuando todas las independientes son cero. Las pendientes (β₁, β₂, etc.) muestran el cambio esperado en la variable dependiente por un incremento de una unidad en la variable independiente correspondiente. Esto hace que la regresión lineal sea valiosa para entender y comunicar cómo se relacionan las variables entre sí.
Limitaciones de la Regresión Lineal
Suposición de linealidad: La regresión lineal asume una relación de línea recta entre la variable dependiente y las variables independientes. Sin embargo, los datos del mundo real a menudo tienen patrones más complejos y no lineales. Cuando la relación real no es lineal, usar regresión lineal puede conducir a predicciones inexactas o resultados engañosos. En tales casos, otros modelos, como la regresión polinómica o los árboles de decisión, pueden proporcionar mejores ajustes.
Sensibilidad a valores atípicos: La regresión lineal es particularmente sensible a los outliers, que son valores extremos que difieren significativamente del resto. Debido a que el modelo intenta ajustar una línea que minimice el error global, un solo outlier puede arrastrar la línea hacia él, distorsionando potencialmente la relación. Esto puede resultar en un modelo inexacto que no represente bien a la mayoría de los datos. Métodos como la regresión robusta o eliminar outliers pueden ayudar a reducir este problema.
¿Qué es la Regresión K-Nearest Neighbors?
La Regresión K-Nearest Neighbors (KNN) es un método utilizado para predecir el valor de una variable objetivo para un nuevo punto de datos observando los puntos más cercanos (o “vecinos”) en el conjunto de datos. A diferencia de modelos como la regresión lineal, que asumen una relación específica entre variables, KNN no asume ninguna forma o estructura particular. En su lugar, basa su predicción directamente en los datos observados. Esto convierte a KNN en un método no paramétrico y basado en instancias — es decir, no intenta construir una fórmula para los datos, sino que utiliza los propios datos para hacer predicciones.
Por ejemplo, imagina que quieres predecir el precio de una casa nueva en función de su tamaño, número de habitaciones y ubicación. KNN observará las casas en el dataset que sean más similares a esa nueva casa y usará sus precios para hacer una predicción.
La regresión KNN implica tres pasos principales:
Elegir el número de vecinos (K): La “K” en KNN representa el número de puntos de datos más cercanos, o “vecinos”, que se utilizan para hacer la predicción. Este es un parámetro que puedes ajustar (un hiperparámetro). Si K = 3, el modelo encontrará los tres puntos más cercanos al nuevo dato. Elegir el valor correcto de K es esencial: un K pequeño puede capturar ruido (sobreajustar) y un K grande puede generalizar demasiado.
Calcular la distancia: Una vez elegido K, el modelo encuentra los K puntos más cercanos al nuevo dato utilizando una métrica de distancia. Una elección común es la distancia euclidiana, que mide la distancia en línea recta entre puntos. Otras métricas incluyen Manhattan y Minkowski.
Predecir: Identificados los K vecinos más cercanos, el modelo realiza una predicción basada en sus valores. En tareas de regresión, esto suele implicar promediar los valores objetivo de esos K vecinos.
Elegir el valor correcto de K
El valor de K impacta significativamente el desempeño del modelo de regresión KNN:
- Valores pequeños de K tienden a ser sensibles a los detalles de cada punto (alto riesgo de sobreajuste).
- Valores grandes de K suavizan la predicción (menos sensibilidad a puntos individuales) pero pueden perder precisión.
Fortalezas de la Regresión KNN
- Simplicidad: KNN es fácil de entender e implementar.
- Adaptabilidad: Al no asumir una relación específica entre variables, puede modelar datos complejos sin demasiada configuración.
- Interpretabilidad: Las predicciones pueden explicarse viendo qué vecinos se utilizaron.
Limitaciones de la Regresión KNN
- Costo computacional: Para cada nueva predicción, KNN debe buscar en todo el dataset para encontrar los K vecinos más cercanos, lo cual puede ser lento si el conjunto de datos es grande. Estructuras como KD-Tree o Ball-Tree ayudan pero siguen siendo intensivas.
- Sensibilidad a características irrelevantes: KNN considera todas las variables por igual al calcular distancias. Si hay variables irrelevantes o en escalas muy distintas, pueden sesgar el resultado. Escalar (Min-Max o estandarización) ayuda.
- Curse of dimensionality: A medida que aumenta el número de variables, la distancia entre puntos pierde significado y se necesitan más datos para que KNN funcione bien. La reducción de dimensionalidad puede ayudar.
KNN es más adecuado cuando: el dataset es relativamente pequeño o se puede buscar de forma eficiente; la relación entre variables y objetivo es compleja o desconocida; los datos están bien escalados y sin demasiadas características irrelevantes; y el problema es apto para un enfoque local.
Formas de mejorar el rendimiento de KNN
- Escalado de datos para mejorar la métrica de distancia.
- Selección de características para eliminar ruido y reducir cómputo.
- KNN ponderado por distancia para dar mayor peso a vecinos cercanos.
- Validación cruzada para elegir K óptimo.
Métodos paramétricos vs. no paramétricos
Los métodos paramétricos hacen suposiciones sobre la forma de la función que mapea las variables de entrada a la salida. Se describen con un número finito de parámetros estimados a partir de los datos (por ejemplo, pendiente e intercepto en regresión lineal). Son eficientes, interpretables y requieren menos datos, pero son menos flexibles y dependen de que las suposiciones sean correctas.
Los métodos no paramétricos no asumen una forma específica. Se adaptan a los datos y pueden capturar relaciones complejas, pero suelen ser más costosos y con mayor riesgo de sobreajuste si no se controlan.
Compensación sesgo-varianza
La compensación sesgo-varianza ayuda a entender el equilibrio entre dos fuentes de error al entrenar modelos:
¿Qué es el sesgo?
El sesgo es el error debido a suposiciones excesivamente simples sobre los datos. Modelos con alto sesgo son demasiado simples (subajuste).
¿Qué es la varianza?
La varianza es el error debido a sensibilidad excesiva a fluctuaciones del conjunto de entrenamiento. Modelos con alta varianza sobreajustan (p. ej., KNN con K muy bajo).
Equilibrar sesgo y varianza
- Sesgo alto, varianza baja: modelos simples (regresión lineal) — estables pero pueden no capturar matices.
- Sesgo bajo, varianza alta: modelos complejos (KNN con K bajo, árboles profundos) — se ajustan fuertemente a los datos de entrenamiento.
- Equilibrio ideal: suficiente flexibilidad sin ser demasiado sensible al ruido.
Técnicas para gestionar la compensación
- Regularización: (Ridge, Lasso) penaliza la complejidad, reduce varianza.
- Validación cruzada: estima desempeño en datos no vistos y ayuda a elegir hiperparámetros.
- Métodos ensemble: bagging (reduce varianza) y boosting (reduce sesgo).
Ejemplo en Python
Importamos librerías y generamos datos para los modelos de regresión lineal y KNN. Usaremos los mismos datos para ambos.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split
# Generación de datos
np.random.seed(0)
X = 2 * np.random.rand(900, 1)
y = 4 + 3 * X + np.random.randn(900, 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
plt.figure(figsize=(11, 6))
plt.scatter(X, y)
plt.title('Datos generados')
plt.xlabel('X')
plt.ylabel('y')
plt.show()
# Modelo de regresión lineal
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
print(f'Intercepto: {lin_reg.intercept_[0]:.2f}')
print(f'Pendiente: {lin_reg.coef_[0][0]:.2f}')
# MSE en prueba
y_pred = lin_reg.predict(X_test)
mse_lin_reg = mean_squared_error(y_test, y_pred)
print('El MSE para prueba es', mse_lin_reg)
mae_lin_reg = mean_absolute_error(y_test, y_pred)
print('El MAE para prueba es', mae_lin_reg)
plt.scatter(X_test, y_test, label='Puntos de datos')
plt.plot(X_test, y_pred, color='orange', linestyle='--', label='Regresión Lineal')
plt.title('Ajuste de Regresión Lineal')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()
# Modelos KNN
from sklearn.neighbors import KNeighborsRegressor
# Creación y entrenamiento de modelos con distintos K
num_neighbors = [3, 9, 15]
for num in num_neighbors:
knn_reg = KNeighborsRegressor(n_neighbors=num)
knn_reg.fit(X_train, y_train)
X_plot = np.linspace(0, 2, 100).reshape(-1, 1)
y_line_pred = knn_reg.predict(X_plot)
y_knn_pred = knn_reg.predict(X_test)
mse_knn = mean_squared_error(y_test, y_knn_pred)
print('MSE de prueba con', num, 'vecinos es', mse_knn)
mae_knn = mean_absolute_error(y_test, y_knn_pred)
print('MAE de prueba con', num, 'vecinos es', mae_knn)
plt.scatter(X_test, y_test, label='Puntos de datos')
plt.plot(X_plot, y_line_pred, color='orange', label='Regresión KNN')
plt.title('Ajuste de Regresión KNN con ' + str(num) + ' vecinos')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()
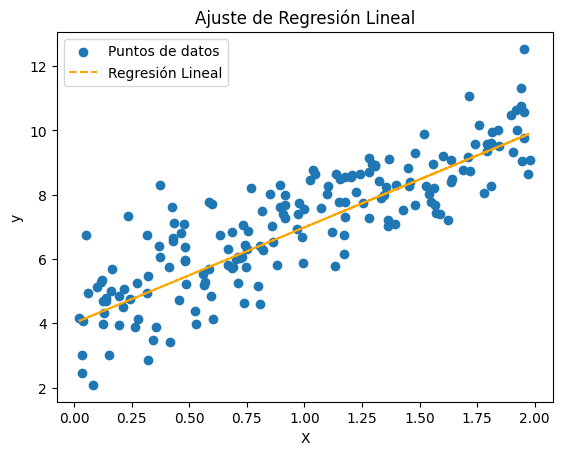
Ajuste de Regresión Lineal
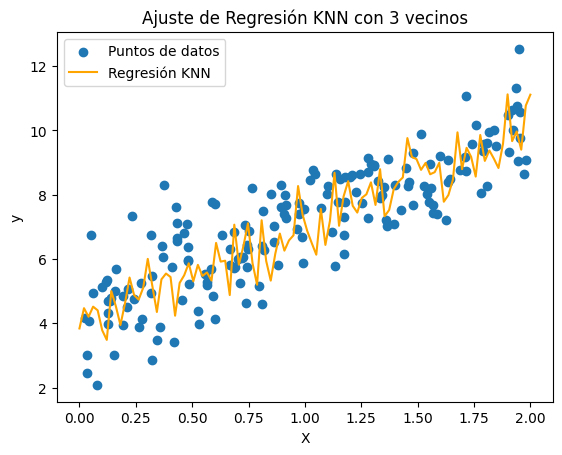
Ajuste de Regresión KNN con K = 3
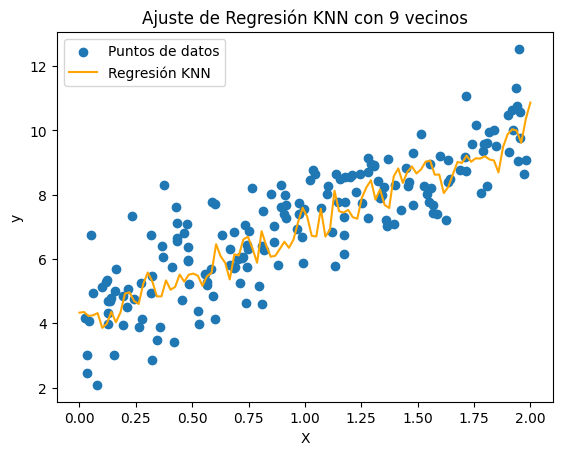
Ajuste de Regresión KNN con K = 9
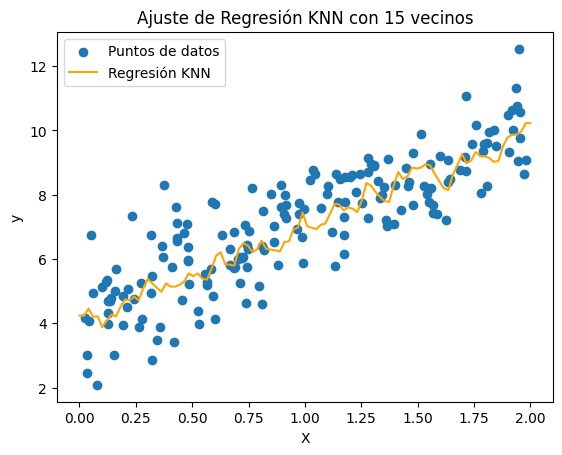
Ajuste de Regresión KNN con K = 15
Resultados de los ajustes
| Modelo | MSE Prueba | MAE Prueba |
|---|---|---|
| Regresión Lineal | 1.07 | 0.82 |
| KNN (n=3) | 1.49 | 0.99 |
| KNN (n=9) | 1.18 | 0.88 |
| KNN (n=15) | 1.14 | 0.86 |
Observaciones de los resultados
Después de construir estos modelos y calcular los valores de MSE para cada uno en los datos de entrenamiento y prueba, observamos que el MSE para la Regresión Lineal en entrenamiento es ligeramente menor que el MSE en prueba, aunque la diferencia no es sustancial. Al examinar los MSE de KNN, vemos que cada modelo tiene un MSE menor en entrenamiento que en prueba, pero las diferencias son mucho mayores. Además, cualquier MSE de entrenamiento de KNN es menor que el MSE de entrenamiento de Regresión Lineal, pero los MSE de prueba de los modelos KNN son todos mayores que el MSE de prueba del modelo de Regresión Lineal.
La evaluación real de un modelo debe basarse en los datos de prueba. Por lo tanto, el modelo de Regresión Lineal funciona mejor para este conjunto de datos, lo cual es de esperar ya que los datos son lineales, como se muestra en la primera imagen. A medida que aumenta el número de vecinos, el MSE de entrenamiento del modelo KNN aumenta, mientras que el MSE de prueba disminuye. Esto indica que el modelo KNN se vuelve menos sensible a los datos de entrenamiento, reduciendo la varianza del modelo.
En situaciones no lineales, KNN puede superar a la regresión lineal porque no asume ninguna forma específica para los datos. Simplemente observa los vecinos más cercanos en el conjunto y hace predicciones basadas en ellos. Como resultado, KNN puede capturar patrones más complejos y proporcionar predicciones más precisas cuando la relación no es una línea recta.
Desafíos de KNN en altas dimensiones
Una de las desventajas significativas de KNN es su sensibilidad a los datos de alta dimensionalidad, un problema conocido como la maldición de la dimensionalidad. En espacios de alta dimensión, cada punto de datos está efectivamente más alejado de los demás porque los datos se “dispersan” en muchas dimensiones. Como resultado, incluso los vecinos más cercanos pueden quedar lejos del punto objetivo, lo que conduce a predicciones deficientes.
Por ejemplo, si tienes un conjunto con 50 observaciones y solo una o dos características, KNN puede encontrar vecinos cercanos con facilidad. Pero si aumentas el número de características a 10, 20 o más, esas 50 observaciones se distribuyen en un espacio mucho mayor, dificultando que KNN encuentre vecinos verdaderamente “cercanos”. En consecuencia, la calidad de la predicción disminuye significativamente a medida que aumentan las características, resultando en un MSE alto para KNN en alta dimensión.
En estos casos, la regresión lineal tiende a funcionar mejor porque no depende de encontrar vecinos cercanos en espacios de alta dimensión. En su lugar, estima las relaciones entre variables en todo el conjunto de datos y bajo la suposición de linealidad, lo cual se mantiene computacionalmente manejable incluso cuando las dimensiones aumentan.
Cuándo elegir Regresión Lineal vs. KNN
En resumen, la elección entre regresión lineal y KNN depende de varios factores:
Cuándo elegir Regresión Lineal
- La relación entre variables es (aproximadamente) lineal.
- Necesitas un modelo simple e interpretable con ideas claras sobre los datos.
- Tu conjunto de datos tiene muchas características (alta dimensionalidad).
- Necesitas predicciones rápidas o tienes recursos computacionales limitados.
Cuándo elegir KNN
- La relación entre variables es probablemente no lineal o compleja.
- No necesitas un modelo altamente interpretable, pero quieres predicciones flexibles.
- Tienes un número pequeño de características y una cantidad moderada de datos.
- Aceptas el costo computacional o dispones de los recursos necesarios.

